|

Ciao, inizio questo ciclo di lezioni con una premessa, un argomento di
base che che è necessario che tu sappia se non vuoi pregiudicare la comprensione
di argomenti più complessi ed interessanti che andrò trattare negli appuntamenti
successivi.
Questa lezione si rivolge in particolar modo a chi conosce scale, arpeggi,…tutto
il materiale al quale si fa riferimento per improvvisare, esclusivamente da un punto
di vista visivo, cioè seguendo la sola posizione, la geometria la diteggiatura del
materiale che dovrai usare.
Questa lezione potrà tornarti utile anche se sei un chitarrista che riconosce
lentamente le note sullo strumento, un musicista che quando va in solo fa riferimento
prevalentemente alle geometrie sulla tastiera seguendo le sole diteggiature del
materiale che si usa per improvvisare, senza sapere il nome e la funzione sugli
accordi delle note che suoni precludendo cosi la possibilità di poter scegliere
consapevolmente le sonorita che vuoi ottenere.
PERCHE DEVI SAPER CALCOLARE GLI INTERVALLI?
TRA I TANTI VORREI INDICARTI ALMENO TRE MOTIVI VALIDI
- Costruire le scale gli accordi e i loro arpeggi velocemente e saperli reperire
in diverse zone della tastiera senza sbagliare, sapendo sempre quali sono le
note che ti occorre suonare.
- Analizzare e capire da quale scala proviene una frase che hai trascritto
dal CD del tuo musicista preferito.
- Capire come sono organizzate le sequenze melodiche che si succedono in questa
frase.
Lavoriamo in questa direzione
Le cose di base: IL CALCOLO DEGLI INTERVALLI
L'intervallo è la distanza che può intercorrere tra due note.
Per calcolare un intervallo è necessario effettuare due calcoli paralleli:
A) Calcolare il grado, cioè il numero progressivo della nota. Ti faccio un
esempio nella scala di Do maggiore.
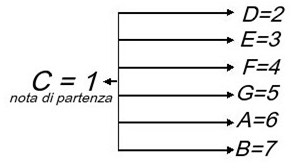
Dallo schema che segue puoi constatare che C è la prima, (cioè la tonica,
la nota di partenza in base alla quale si calcolano tutte le altre distanze) D è
la seconda, E la terza e così via.
Naturalmente questo primo conteggio può e deve
essere effettuato partendo da qualsiasi nota. Se ad esempio parti da E, F sarà la
seconda nota, G la terza, A la quarta e così via.
Considera che questo primo calcolo ti da solo il nome generico dell'intervallo,
questo è determinato dal numero di ordine della nota rispetto a quella di partenza,
ad esempio G è la quinta nota a partire da C, D è la quarta nota a partire da A.
Per considerare l'intervallo in modo completo devi però ricorrere ad un secondo
calcolo che ne determinerà la qualità.
B) Calcolare la qualità dell'intervallo
Nel costruire una scala o un accordo ti troverai di fronte all'esigenza di considerare
differenti possibilità per una stessa famiglia di intervalli. Questo dipende dal
numero dei toni e semitoni che intercorrono nella distanza tra due note.
A questo punto potrai notare che la misurazione di un intervallo oltre al numero
progressivo della nota (cioè la seconda, la terza, la quarta a partire da…) implica
un ulteriore operazione di calcolo:valutare la distanza effettiva tra le note.
Questa distanza sarà espressa ed avrà come unità di misura: toni, semitoni e
loro somme. Vediamo un esempio che riguarda gli intervalli di quinta.
Consideriamo tre intervalli con lo stesso nome comune, ma di qualità diversa:
quinta diminuita, quinta giusta e quinta aumentata. Procediamo per tappe separate.
- In base al primo calcolo puoi determinare che la quinta nota a partire da
C è G, questo nome sarà comune ai tre intervalli di quinta menzionati.
- Ora vediamo dove è la differenza. Una quinta diminuita deve distare dalla
nota di partenza tre toni, una quinta giusta tre toni e mezzo, una quinta aumentata
quattro.
- La distanza da C a G è di tre toni e mezzo ciò corrisponde ad un intervallo
di quinta giusta.
- Per avere l'intervallo di quinta diminuita applicherai il bemolle alla nota
G. In questo modo puoi accorciare la distanza a tre toni richiesti ed ottenere
un intervallo di quinta diminuita (C > Gb)
- Per avere l'intervallo di quinta aumentata applicherai il # a G. In questo
caso la distanza si estende a 4 toni ed avrai l'intervallo di quinta aumentata(C
> G#).
- Per rettificare le distanze ed ottenere gli spazi appropriati ad un determinato
intervallo, devi applicare l'alterazione sempre alla seconda nota della coppia
e non alla prima. Quando costruirai una scala se fai questo errore rischierai
di avere un'altra scala al posto di quella che ti occorre.
- Ora l'intervallo è completo. Sai che G è la quinta di C e grazie alle varie
distanze hai determinato tre differenti qualità per gli intervalli di quinta.
Ecco una tavola che riassume gli intervalli più importanti, memorizzali, ti
saranno utili per molte cose.
| sigla numerica |
Nome intervallo |
distanza |
Esempio
1 |
Esempio
2 |
commento |
| 1 |
unisono |
nessuna |
C1 > C1 |
Eb1 > Eb1 |
stessa nota |
| b2 |
seconda minore |
ST |
C > Db |
Eb > Fb |
|
| 2 |
seconda maggiore |
T |
C > D |
Eb > F |
|
| #2 |
Seconda aumentata |
T + ST |
C > D# |
Eb > F# |
nota enarmonica |
| b3 |
terza minore |
T + ST |
C > Eb |
Eb > Gb |
nota enarmonica |
| 3 |
terza maggiore |
2 T |
C > E |
Eb > G |
|
| 4 |
quarta giusta |
2 T + ST |
C > F |
Eb > Ab |
|
| #4 |
quarta aumentata |
3 T |
C > F# |
Eb > A |
nota enarmonica |
| b5 |
quinta diminuita |
3 T |
C > Gb |
Eb > Bbb |
nota enarmonica |
| 5 |
quinta giusta |
3 T + ST |
C > G |
Eb > Bb |
|
| #5 |
quinta aumentata |
4 T |
C > G# |
Eb > B |
nota enarmonica |
| b6 |
sesta minore |
4 T |
C > Ab |
Eb > Cb |
nota enarmonica |
|
6 |
sesta maggiore |
4
T + ST |
C > A |
Eb
> C |
nota enarmonica |
|
bb7 |
settima diminuita |
4
T + ST |
C > Bbb |
Eb
> Dbb |
nota enarmonica |
| b7 |
settima minore |
5 T |
C > Bb |
Eb > Db |
|
| 7 |
settima maggiore |
5 T + ST |
C > B |
Eb > D |
|
| 8 |
ottava |
6 T |
C1 > C2 |
Eb1 > Eb2 |
dista un ottava |
- Dalla tavola puoi notare che esistono note che hanno uno stesso suono
ma un nome differente (ad esempio F#, Gb),queste assumono il nome di note enarmoniche.
- La presenza di note enarmoniche può generare degli intervalli enarmonici
(es Eb > F# / Eb > Gb). Infatti in questa tavola troverai delle coppie di note
che sono catalogate con un differente nome di intervallo anche se hanno lo stesso
suono e la stessa distanza.
- La presenza di note ed intervalli enarmonici sono segnalate in grigio,
gli intervalli di 6 e bb7 sono evidenziati in nero
Un ulteriore chiarimento:
- se prendi in considerazione la distanza posta tra C e D# o C e Eb, puoi
notare che suonando i due intervalli ottieni lo stesso motivo. Tuttavia i due
intervalli hanno un nome differente.
- Questa diversità nel nominare l'intervallo è data dalla differenza di
nome delle note D# e Eb.
Osserva: D, in questo caso diesis, è la seconda nota a partire da C mentre E,
in questo caso bemolle,è la terza nota a partire da C. E' questo che fa la differenza.
Ed è per questo motivo che D# è una SECONDA aumentata e Eb
è una TERZA minore. Come puoi vedere è il grado, inteso come numero di
ordine dalla nota di partenza, a determinare il nome dell'intervallo,mentre
la distanza determina solo la qualità.
- Questo ragionamento vale per gli altri intervalli enarmonici presenti
nella tavola.
- Sempre per non rischiare di confonderti le idee, ho ritenuto opportuno
includere in questa tavola solo gli intervalli di uso comune, escludendone altri
che non saranno utilizzati.
Usiamo gli intervalli per costruire le scale
Vorrei farti constatare quanto sia importante padroneggiare gli intervalli utilizzandoli
per un'applicazione decisamente utile alla pratica strumentale: costruiamo le scale.
Partiamo da un presupposto, un esigenza reale.
Hai un accordo di C7 e vuoi suonarci sopra qualcosa dal sapore blues.
Ti accorgi che spesso ti capita di suonare note sbagliate perchè non riesci a ricordare
bene le diteggiature della scala blues che ti ha mostrato il tuo amico qualche giorno
fa.
C'è qualcosa di meglio per evitare di suonare note sbagliate:
- Step one. Sapere e tenere bene in mente quali sono le note corrette
- Step two. Trovarle sul tuo strumento, ed inserirle senza sbagliare e senza
troppe difficoltà nelle frasi.
Per ora occupiamoci del primo step. Il primo passo per non inserire note errate
nelle tue frasi consiste nel sapere con decisione quali sono quelle che devi andare
a suonare.
Non parlo di tasti e posizioni, che rappresentano un elemento secondario, intendo
dire: stampa nel tuo cervello il nome delle note che ti servono per suonare correttamente.
Ti faccio un esempio con la scala blues minore. Anche questa scala è costituita
da note che sono poste ad una determinata distanza (intervallo) dalla tonica.
Queste distanze sono riportate nello schema che segue ed applicate alla tonica C
per ottenere le note che fanno parte della scala di C blues minore.
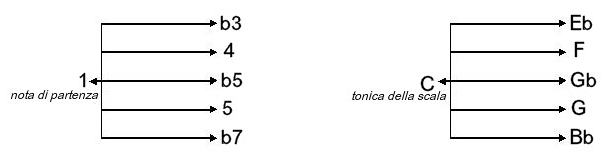
Come hai visto puoi costruire una scala calcolando gli intervalli che la caratterizzano
partendo dalla sua tonica. Seguendo questo metodo stai applicando la sua formula.
Ora, se vuoi usare la scala blues minore sovrapposta all'accordo di C7, sai quali
sono le note giuste da suonare. Poniti come obbiettivo di suonare quelle note
consapevole del loro nome e non soltanto del numero del tasto. Devi farlo anche
se questo ti costringerà a suonare una nota al minuto. Questo vuol dire che all'inizio
farai grandi melodie con delle bellissime note lunghe e con il tempo potrai suonare
veloce senza sbagliare più nota.
" Si fa per dire!"
Con gli intervalli puoi costruire tutte le scale, anche
le più difficili
Ti vorrei proporre un ulteriore dimostrazione per utilizzare gli intervalli quando
costruisci le scale.
Proviamo con la scala diminuita semitono – tono (ST -T)
|

|
|
(nb b5 e #4 cioè Gb e F# hanno lo stesso suono)
|
|
Formula della scala diminuita ST - T
|
Applicazione della formula
|
Ho inserito la costruzione della scala diminuita soltanto per dimostrarti
che con questo metodo si possono costruire tutte le scale, anche quelle dedicate
ai musicisti di livello avanzato
Appurato questo discorso se sai i nomi delle note che puoi suonare pigiando i tasti
del tuo strumento, potrai trovare le note che fanno parte delle scale che abbiamo
visto..
Da ora in poi usa questo sistema per tutte le scale gli accordi e gli arpeggi.
Ora usiamo gli intervalli per capire quali scale sono state
utilizzate nel suonare una frase che abbiamo trascritto da un brano

Se vai a constatare la distanza intervallare che intercorre tra ciascuna nota della
frase e la tonica dell'accordo che ti accompagna (inquesto caso C7) puoi ottenere
le formule delle scale a cui si è fatto riferimento per improvvisare la frase, vediamo
quali:
- nella prima battuta hai 1,2,b3,5,6 e b7. Se conosci gli intervalli che formano
la scala dorica (1,2,b3,4,5,6,b7) puoi facilmente capire che in questa battuta
si è utilizzata la scala di C dorico senza suonare la quarta. Quindi si tratta
di sovrapposizione di scala dorica partendo dalla tonica dell'accordo dominante.
In questo caso la b3 assume la funzione di tensione #9.
- Nella seconda battuta della frase le cose si fanno più complesse e sempre
con lo stesso metodo puoi riconoscere la formula della scala diminuita ST-T:
1,b2,#2,3 #4 (che corrisponde anche alla b5) 6, b7
In questo caso la scala di riferimento per questa frase è stata C diminuita
ST – T.
Adesso sempre grazie agli intervalli possiamo anche analizzare
e capire gli elementi che caratterizzano il fraseggio, quindi il movimento melodico
della frase.
Questo è importante perche sapere la scala non significa suonare bene.
Se sopra agli accordi ti limiti ad eseguire soltanto la scala o dei frammenti di
essa nel tuo solo finirai per suonare soltanto delle note giuste, niente di più.

Analizziamo la frase punto per punto seguendo le lettere minuscole tra parentesi:
(a) Si tratta di due cellule melodiche dal percorso simile che partono da due
note diverse della scala: nel primo caso hai D come nota di partenza poi si sale
alla nota successiva in scala e si ritorna alla precedente (questa tecnica be bop
si chiama upper neighbor) seguono due note discendenti della scala poi si scende
di un intervallo di terza minore cioè da Bb a G. La seconda cellula come vedi è
molto simile alla precedente, inizia con un upper neighbor (note A, Bb, A) e discende
fino a E. L'unica differenza?
Non c'è il salto di terza tra le ultime due note. Quando si suona una cellula seguita
da un'altra modificata partendo da diversi punti di una scala hai applicato il concetto
di sviluppo melodico. Questo è un elemento importante per creare interesse nei soli.
(b) In questo punto si suonano tre note in ordine scalare, è un semplice frammento
di scala.
(c) Questo è un intervallo di terza diatonico alla scala utilizzata con
ritorno alla nota di partenza (C, Eb,C) seguito da una serie cromatica di tre note
(Db,D,eEb) che approccia la terza dell'accordo. Gli approcci cromatici da sotto,
sulla nota dell'accordo, sono altri elementi che provengono dallo studio del fraseggio
be bop.
(d) Qui si ripete per due volte l'intervallo di terza minore (E,G)
(e) Ancora una tecnica di approccio be bop: ecco un singolo approccio cromatico
da sotto sulla nota dell'accordo in questo caso è A ad approcciare Bb, la b7 di
C7.
In questo modo puoi riconoscere e capire le tecniche di fraseggio utilizzate nei
soli ed applicarle in altri contesti, questo metodo di lavoro fa parte degli stidi
di frammentazione melodica.
Bene, è tempo di concludere un augurio di buon lavoro.
Arrivederci alla prossima lezione.
Gli argomenti trattati da Paolo Patrignani sono svilippati
nelle sue pubblicazioni didattiche distribuite dalla Universal
Oltre l'arpeggio - BMG Publications MLR 512
Provaperta - Ricordi MLR 670
I due metodi includono un cd audio di supporto per saperne di più
www.ladybirdproject.com/paolopatrignani/home.htm

| 05/04/2017 | LEZIONI (chitarra): (B. Patterson, T. De Caprio, M. Ariodante, G. Continenza, G. Continenza, G. Fewell, N. Di Battista, A. Ongarello, D. Comerio, A. Tarantino, S. Khan, A. Bonardi, M. Falcone, A. D'Auria) |
|
Inserisci un commento
© 2010 Jazzitalia.net - Paolo Patrignani - Lady Bird Project -
Tutti i diritti riservati
|
© 2000 - 2026 Tutto il materiale pubblicato su Jazzitalia è di esclusiva proprietà dell'autore ed è coperto da Copyright internazionale, pertanto non è consentito alcun utilizzo che non sia preventivamente concordato con chi ne detiene i diritti.
|
Questa pagina è stata visitata 18.879 volte
Data pubblicazione: 27/02/2010

|
|

