INDICE LEZIONI

Parte prima - Teoria generale: I fondamenti dell'armonia tonale di Paolo Guiducci

Lo scopo di questa sezione è principalmente quello di esaminare gli elementi che stanno alla base dell'evoluzione della musica occidentale. Ovvero come sono state organizzate le altezze e quali sono state le ragioni. È essenziale questa conoscenza soprattutto per capire i perché della musica di oggi. Non siamo in grado, ne tuttavia ha importanza in questa sede, di valutare con certezza in quale maniera i pionieri della musica sono arrivati a certe conclusioni. Può essere stata una conseguenza diretta del fenomeno degli armonici così come un'intuizione o una casualità. Oppure, come più probabile, tutte e tre le cose insieme. Quello che viene messo in evidenza in questa sezione sono solo i passi fondamentali, non viene offerto perciò un quadro storico esauriente sull'argomento.

Gli armonici
Prima di parlare di armonici è importante definire il concetto di suono puro. La forma d'onda di un suono puro è una sinusoide semplice, come quella rappresentata in figura 1 (a). I suoni esistenti in natura sono suoni complessi, i quali sono scomponibili in una serie di suoni puri chiamati armonici. Gli armonici (chiamati anche armoniche, ipertoni, parziali o formanti) sono generati spontaneamente dalla vibrazione dei corpi elastici. L'armonico più grave (più basso), chiamato anche armonico fondamentale, determina l'altezza del suono complesso mentre gli armonici superiori (più acuti) ne determinano il timbro in base alla loro intensità relativa. Vediamo ora, molto sinteticamente, come avviene fisicamente tale fenomeno.

Classificare le varie timbriche è un'impresa ardua, si possono tuttavia riassumere alcuni aspetti soggettivi del timbro:

• I suoni puri hanno un carattere che può essere definito come vuoto o neutro. Oppure, a seconda dei punti di vista, limpido e cristallino. Ad esempio il suono del diapason e dell'ocarina sono quasi puri.
  
• I suoni con un limitato numero di armonici (diciamo dal primo al sesto o settimo) sono più ricchi e pastosi dei suoni puri, pur mantenendo un carattere dolce e morbido. Ad esempio i registri medi del pianoforte, il flauto e l'oboe.
  
• I suoni ricchi degli armonici più elevati, soprattutto se molto intensi, conferiscono al suono un carattere aspro e frizzante. Ad esempio il violino e la chitarra elettrica distorta.
  
• I suoni poveri di armonici pari (ovvero gli armonici 2°, 4°, 6°, ecc.) tendono ad acquisire un tono nasale, tipico del clarinetto.

Figura 1: Esempi di forme d'onda dei suoni contenenti fino a cinque armonici, calcolate in modo sintetico. La freccia a due punte indica la durata (T) del periodo dell'armonico fondamentale. Esso corrisponde anche alla durata di un ciclo completo, per ogni esempio sono riportati due cicli completi. Il calcolo delle sinusoidi è stato effettuato riducendo di un fattore 5/4 l'ampiezza degli armonici man mano che si sale in quelli più alti. (a) Forma d'onda sinusoidale corrispondente ad un suono puro. Tale suono contiene solo un armonico fondamentale con frequenza diciamo f. (b) Forma d'onda risultante dalla somma dei primi due armonici: f+2f. (c) Somma dei primi tre armonici: f+2f+3f. (d) Somma dei primi quattro armonici: f+2f+3f+4f. (e) Somma dei primi cinque armonici: f+2f+3f+4f+5f.

• L'intensità del primo armonico è fondamentale per dare pienezza al suono. In genere nel violino, nella chitarra distorta e nei suoni molto gravi, il primo armonico è meno intenso degli armonici immediatamente successivi.
  
• In linea di massima il secondo armonico conferisce limpidezza al suono. Il sesto e l'ottavo lo rendono chiaro e squillante. Il settimo e il nono lo inaspriscono. Il decimo ne aumenta la chiarezza dando al suono un'impronta metallica.

Molti strumenti musicali permettono di influenzare, entro certo limiti, la disposizione e l'intensità degli armonici. Per quanto riguarda gli strumenti a corde, ad esempio, è sufficiente fare alcuni semplici esperimenti con la chitarra. Per rendesi conto meglio delle differenze timbriche consiglio di suonare sempre la stessa nota, ad esempio il La della quinta corda a vuoto:

• Se la corda viene pizzicata con forza il suono, oltre ad essere più intenso, risulta più ricco di armonici rispetto a quando viene pizzicata piano.
  
• Il suono emesso dalla corde è più ricco di armonici nella fase iniziale che in quella finale. In pratica il suono altre a spegnersi gradualmente si impoverisce più in fretta degli armonici più alti.

Figura 2: Forme d'onda emesse della quarta corda a vuoto (Re) della chitarra elettrica. L'esempio (a) si riferisce al suono pulito mentre l'esempio (b) al suono distorto. La freccia a due punte indica la durata (T) del periodo dell'armonico fondamentale. Nel suono distorto l'onda è più spigolosa e sconnessa di quella del suono pulito. Queste caratteristiche indicano che il suono contiene molti armonici superiori e relativamente intensi. Una caratteristica tipica di tutti gli strumenti a corde sta nel fatto che il suono emesso subisce una metamorfosi continua. In entrambe le onde infatti il secondo periodo è leggermente diverso dal primo e continuerà a cambiare lungo il suo percorso. La causa di questo è l'inarmonicità tipica della vibrazione delle corde, anche se in misura minima. Tali esempi sono perciò puramente indicativi, la forma d'onda può infatti cambiare visibilmente se prelevata in tempi diversi.

• Se la corda viene pizzicata esattamente a metà della sua lunghezza il suono risulta impoverito degli armonici pari e acquisisce un carattere nasale. Questo avviene perché il plettro indirizza la corda a non formare nodi nel punto in cui viene pizzicata e gli armonici pari formano tutti un nodo a metà corda.
  
• Se la corda viene pizzicata in punti sempre più vicini al ponte il suono si arricchisce di armonici sempre più alti, diventa cioè più squillante. Questo caratteristica è evidente in modo particolare sulle note più basse.
  
• È possibile vincolare la corda a vibrare solo in alcuni dei suoi modi vibrazionali, ottenendo così l'emissione solo di certi armonici. Se la corda viene pizzicata appoggiando leggermente un dito della mano sinistra in un altro punto della corda stessa, verranno attivati solo i modi vibrazionali che hanno un nodo nel punto di contatto. La corda va toccata facendo attenzione che non appoggi sui tasti. Dopo aver pizzicato la corda occorre togliere subito il dito appoggiato, per evitare di smorzare la vibrazione troppo in fretta. Se ad esempio vogliamo ottenere il terzo armonico, ed i suoi multipli, il dito va appoggiato in uno dei punti che suddividono idealmente la corda in tre parti uguali (in questo caso il punto esatto corrisponde al settimo tasto). Anche se vengono attivati tutti i modi vibrazionali che hanno un nodo nel punto di contatto, risulta preponderante l'armonico più basso. Il suono risultante è perciò molto vicino al suono puro.
  
• I suoni più bassi sono più ricchi di armonici rispetto a quelli più alti. Le note delle due ottave più basse di un pianoforte, ad esempio, possono contenere anche più di 30 armonici udibili. Al contrario le note delle due ottave più alte contengono dai due ai quattro armonici.

Quando gli armonici di un suono sono esatti, ovvero multipli interi dell'armonico fondamentale, la sensazione è quella di una completa fusione in un suono complesso. Al contrario se gli armonici non sono esatti abbiamo un suono enarmonico (ad esempio il suono delle campane). Se infine nella disposizione degli armonici subentrano fattori di casualità abbiamo un rumore (ad esempio il suono del rullante a cordiera). Ovviamente è impossibile definire un confine preciso che permetta di distinguere un suono da un rumore. È bene infatti precisare che anche negli strumenti musicali ad intonazione determinata i fenomeni di enarmonia e casualità sono sempre presenti, seppur in misura minima. In ogni caso in questa sezione si farà riferimento esclusivamente ai suoni aventi armonici esatti.

È logico a questo punto chiedersi in che modo l'orecchio attribuisce una precisa altezza ai suoni complessi, considerando che essi sono la fusione di tanti suoni aventi altezze diverse. Senza addentrarsi troppo nell'argomento, di cui fra l'altro non ci sono ancora risposte certe, sembra che l'orecchio operi sul suono una specie di analisi armonica. L'orecchio cerca perciò di individuare nel suono una serie regolare di armonici, da cui viene calcolata una altezza virtuale che normalmente corrisponde all'armonico fondamentale. Questo avviene anche se l'armonico fondamentale è di fatto meno intenso degli altri o addirittura inesistente. Nel suono delle campane tubolari, ad esempio, l'altezza virtuale attribuita dall'orecchio è in realtà inesistente. Tale suono contiene in genere tre armonici piuttosto intensi aventi rapporti molto simili agli armonici 2°, 3° e 4°, in base ad essi viene poi calcolata l'altezza corrispondente al 1° armonico virtuale. Nel caso di suoni fortemente enarmonici l'orecchio può perdere tale capacità, di conseguenza gli armonici non verranno più percepiti come fusi in un solo suono ma separatamente.

Le scale di giusta intonazione
Il problema principale dell'armonia è la sovrapposizione dei suoni, ovvero con quale criterio sovrapporre i suoni per rendere il tutto piacevole all'ascolto. I primi accostamenti di suoni sono avvenuti utilizzando gli intervalli più consonanti, aggettivo già menzionato nella tabella degli intervalli. Sono considerate consonanti le note che suonano insieme come se costituissero un corpo unitario. Le prime sovrapposizioni sono avvenute presumibilmente con le voci all'unisono o a distanza di ottava, la voce maschile si occupava del basso e quella femminile dell'ottava alta. Successivamente è stata scoperta anche l'alta consonanza presente nell'intervallo di quinta giusta. Cerchiamo ora di capire a cosa è legato il senso di consonanza, il quale è percepibile dall'orecchio in modo chiaro. Esaminiamo i primi nove armonici riportati sulla tabella 1.

Tabella 1: Primi nove armonici di un Do avente frequenza f. Nella prima colonna è riportato il numero progressivo dell'armonico. Successivamente abbiamo la frequenza dell'armonico (rappresentata come multipli di f e l'ottava a cui appartiene (considerando la fondamentale appartenente alla prima ottava). Nella quarta colonna è riportata la frequenza dell'armonico abbassata delle ottave necessarie per rientrare nella prima ottava (in pratica occorre dividere per due fino ad ottenere una frazione che sia compresa fra uno e due). Nelle ultime due colonne abbiamo rispettivamente l'intervallo effettivo dell'armonico (riportato come intervallo semplice) e la nota considerando il Do come fondamentale. Il 7° armonico, Sib, è contrassegnato da (*) in quanto è calante rispetto a quello calcolato nella scala minore giusta. Notare che gli armonici 4, 5 e 6 (evidenziati in grassetto) corrispondono all'accordo maggiore della fondamentale, Do-Mi-Sol. Una visualizzazione più estesa degli armonici è riportata nella figura 7.

Prima di procedere è importante avere chiaro il seguente concetto: le frequenze dei vari intervalli sono sempre matematicamente proporzionali. Questo significa che l'intervallo fra due frequenze è dato dal loro rapporto non dalla differenza. Ad esempio l'intervallo fra 2f e 3/2f è dato da: 2: 3/2 = 4/3.

Il secondo armonico ha frequenza 2f, ovvero l'ottava del suono fondamentale. Se analizziamo due suoni distinti a distanza di ottava possiamo verificare che gli armonici del suono più alto sono tutti presenti nel suono più basso (vedi tabella 3.22). Questa è la ragione per cui tali suoni sono stati definiti pienamente consonanti e chiamati perciò con lo stesso nome. L'intervallo di ottava delimita anche l'ambito su cui verranno effettuate le ulteriori suddivisioni (è interessante valutare come questo principio musicale di base sia presente in quasi tutte le culture musicali).

Il terzo armonico ha frequenza 3f, se lo abbassiamo di un'ottava (dividendolo a metà) otteniamo uno suono con frequenza 3/2f, il quale rientra nell'ambito dell'ottava ovvero fra 1f e 2f. Questo suono, è in pratica la prima divisione dell'ottava e corrisponde all'intervallo di quinta giusta. Tale intervallo introduce anche il suo complementare, la quarta giusta. Per calcolare la frequenza di un intervallo complementare occorre dividere l'ottava per l'intervallo di partenza. In questo caso avremo: 2: 3/2 = 4/3f. Abbiamo così ottenuto la prima suddivisione riportata in figura 3. Essa contiene le cosiddette consonanze perfette con la fondamentale: l'ottava, la quinta giusta e la quarta. Li chiameremo gradi centrali.

A questo punto si potrebbe pensare che la consonanza sia legata agli intervalli esistenti fra la fondamentale e gli armonici più vicini. In realtà le cose non stanno esattamente così, la consonanza è si legata agli armonici più bassi ma in relazione ai rapporti che si formano fra armonici adiacenti, non con la fondamentale. Per esempio:

• Intervallo fra 1° e 2° armonico. E' rappresentato dal rapporto 2/1, è denominato ottava ed è una consonanza perfetta.
• Intervallo fra 2° e 3° armonico. E' rappresentato dal rapporto 3/2, è denominato quinta giusta ed è una consonanza perfetta.
• Intervallo fra 3° e 4° armonico. E' rappresentato dal rapporto 4/3, è denominato quarta giusta ed è una consonanza perfetta.
• Intervallo fra 4° e 5° armonico. E' rappresentato dal rapporto 5/4, è denominato terza maggiore ed è una consonanza imperfetta.
• Intervallo fra 5° e 6° armonico. E' rappresentato dal rapporto 6/5, è denominato terza minore ed è una consonanza imperfetta.

Abbiamo in questa maniera introdotto le rimanenti due consonanze chiamate imperfette, esse sono la terza maggiore e la terza minore. Sono consonanti allo stesso modo anche gli intervalli complementari ad essi e sono tutti elencati nella tabella 2. Gli intervalli non menzionati nella suddetta tabella sono denominati dissonanti (escluso quelli che possono essere considerati come consonanze leggermente fuori tono).

Facciamo ora un piccolo passo indietro. Nella tabella 1 è visibile una cosa molto importante: gli armonici 4°, 5° e 6° corrispondono a Do, Mi e Sol, ovvero alla prima, terza maggiore e quinta giusta. Si tratta perciò della triade maggiore. Questo primo accordo presente già in natura è il fondamento dell'armonia tonale occidentale. Il passo successivo è stato infatti quello di applicare la triade maggiore sui gradi centrali rappresentati in figura 3 (prima, quarta giusta e quinta giusta) e ricavare così le note rimanenti della scala maggiore.

Figura 3: Gradi centrali. Per facilitare la lettura al di sopra dei rapporti sono riportate le note considerando il Do come suono fondamentale. È opportuno sottolineare che tali denominazioni sono state introdotte in seguito. Le linee oblique indicano nella congiunzione il rapporto fra le due note relative. L'intervallo calcolato fra Fa e Sol (3/2: 4/3 = 9/8) è di un tono.

Tabella 2: Elenco consonanze. Sono stati raggruppati gli intervalli complementari, ad esempio la sesta minore è complementare alla terza maggiore. In tabella 3.3 è riportata la caratteristica sonora di tutti i gradi.

Le frequenze della terza maggiore e quinta giusta in relazione alla fondamentale sono rispettivamente 5/4f (Mi) e 3/2 f (Sol). In relazione alla quarta sono: 4/3 * 5/4 = 5/3 f (La), 4/3 * 3/2 = 2f (Do). In relazione alla quinta sono: 3/2 * 5/4 = 15/8 f (Si), 3/2 * 3/2 = 9/4 f (Re). Occorre abbassare il Re di un'ottava in quanto 9/4 è superiore a 2, dividendolo per due otterremo perciò: 9/8 f. Il Re corrisponde anche al nono armonico. Abbiamo a questo punto ottenuto la scala maggiore di giusta intonazione, o semplicemente giusta, il genitore della attuale scala maggiore. Essa è rappresentata nella figura 4 con tutti i rapporti fra i vari gradi.

Figura 4

I toni interi sono circa il doppio dei semitoni, è perciò possibile dividerli per ricavare le cinque note mancanti: Do#/Reb, Re#/Mib, Fa#/Solb, Sol#/Lab, La#/Sib. Tali note sono ricavabili in diverse maniere. Ad esempio il Sol# può essere calcolato come la terza maggiore del Mi ossia: 5/4 * 5/4 = 25/16. Se invece vogliamo ricavare il Lab (enarmonico di Sol#) può essere calcolato come terza minore del Fa ovvero: 4/3 * 6/5 = 8/5. I risultati sono perciò diversi, con l'avvento del sistema temperato queste differenze saranno eliminate (vedi sezione "La scala temperata").

Nella scala maggiore giusta viene privilegiato l'intervallo di terza maggiore, da essa infatti possono essere costruite tre triadi maggiori perfettamente intonate: Do maggiore, Fa maggiore e Sol maggiore. Moltissimi brani sono armonizzati esclusivamente con questi tre accordi.

Se al contrario venisse privilegiata la terza minore (l'altra consonanza imperfetta) ed applicassimo sui gradi centrali (figura 3) la triade minore, otteniamo la scala minore di giusta intonazione. Tale scala, riportata in figura 5, è anche il genitore della attuale scala minore naturale:

Figura 5

Nella scala di figura 5 sono riportati solo i rapporti fra le note adiacenti. Se confrontiamo l'ordine di questi rapporti con quelli della scala maggiore giusta partendo dalla nota La (9/8, 16/15, 9/8, 10/9, 16/15, 9/8, 10/9), è chiaro che si tratta di una successione molto simile, anche se non identica. Nel sistema temperato, con l'annullamento della differenza fra tono grande e tono piccolo, le successioni diventano identiche (vedi sezione "La scala temperata"). In ogni caso è da questa osservazione che è nato il concetto di relativa minore, che nel caso del Do maggiore è il La minore ovvero il sesto grado (vedi sezione "La scala minore naturale").

Per ragioni di chiarezza riepilogo gli intervalli delle scale giuste presenti effettivamente nella disposizione degli armonici naturali: l'ottava (2° armonico), la quinta giusta (3° armonico), la terza maggiore (5° armonico), la nona maggiore (9° armonico).

È opportuno a questo punto fare una precisazione. La triade maggiore presente negli armonici naturali (4°, 5° e 6° armonico) è formata da tre suoni puri, in quanto ogni armonico è un suono puro. Nella musica in realtà vengono effettuate sovrapposizioni di suoni complessi, ogn'uno dei quali, come abbiamo visto, è formato da una propria serie regolare di armonici. Il risultato è perciò molto differente. Riporto di seguito, in modo sintetico, una analisi di quello che avviene. Quando due suoni complessi di altezza diversa vengono sovrapposti possono verificarsi due situazioni: gli armonici con frequenza identica si sommano, gli altri si posizionano in zone intermedie. Se consideriamo il suono più basso come quello fondamentale abbiamo, nel primo caso, una serie di armonici rafforzati. Nel secondo caso abbiamo invece nuovi armonici che non seguono la stessa regolarità di quelli del suono fondamentale. Consideriamo ora il fatto che nella musica sono abitualmente presenti successioni e sovrapposizioni di ben più di due suoni. Inoltre tali suoni possono essere leggermente fuori tono (vedi ad esempio la scala temperata, sezione "La scala temperata") ed avere timbriche radicalmente diverse. È evidente che si tratta di un argomento molto complesso, il quale coinvolge direttamente la capacità discriminatoria soggettiva del cervello umano sui suoni e le timbriche. La psicoacustica è la scienza che si occupa di questi problemi, un settore di studio che ha più domande aperte che non risposte.

Considerazioni sulle scale di giusta intonazione
Da oltre due secoli le scale giuste non vengono praticamente più utilizzate, eccezione fatta per le riletture di musica antica fedeli all'originale. Tuttavia l'analisi di queste scale permette di capire le ragioni di molte regole e abitudini della musica tonale:

• La ragione per cui la scala maggiore e la minore naturale hanno avuto una diffusione più ampia rispetto ad altre scale.
  
• La ragione per cui tantissimi brani sono armonizzati esclusivamente con i tre accordi maggiori costruiti sui gradi centrali: prima, quarta e quinta. In particolar modo nella musica folk, blues e rock&roll. Tanti esempi sono poi anche nella musica rock e leggera.
  
• Perché gli intervalli sono chiamati giusti, maggiori o minori. Gli intervalli giusti (prima, quarta e quinta) sono quelli più consonanti e derivati direttamente dai primi tre armonici naturali. Essi sono anche i gradi centrali su cui vengono costruite le scale giuste. Gli intervalli di terza, sesta e settima possono essere maggiori o minori. Sono maggiori quelli che appartengo alla scala maggiore e minori quelli che appartengono alla scala minore. L'unica eccezione riguarda l'intervallo di seconda, il quale viene chiamato maggiore o minore anche se nelle due scale è sempre maggiore. È infatti più logica questa denominazione in quanto la seconda è complementare alla settima (vedi sezione "Intervalli complementari"), la quale può essere a sua volta maggiore o minore.
  
• La ragione per cui gli accordi vengono costruiti sulle scale per intervalli di terza (sezione 3.3.1). In realtà questa regola è una convenzione. Come abbiamo visto, sono le scale che derivano dagli accordi non viceversa. In origine c'era l'accordo maggiore e minore, la denominazione degli intervalli (prima, terza, quinta) è stata introdotta in un secondo momento quando, per comodità, si è preferito considerare la scala come punto di partenza.

Le scale giuste non sono le uniche ad essere state utilizzate in passato. Ne esistevano infatti altre molto simili anche se costruite con criteri differenti. Un particolare accenno va fatto alla scala maggiore pitagorica, nella quale le suddivisioni sono ricavate applicando una quinta (intesa come rapporto 3/2) sotto al Do e cinque quinte consecutive sopra (sempre partendo dal Do). Le note ottenute sono in ordine: Do, Fa, Sol, Re, La, Mi, Si. Tali note devono essere poi riportate all'interno della prima ottava. In pratica sono le stesse note della scala maggiore giusta, anche se i rapporti calcolati risultano leggermente diversi. Di conseguenza contiene un numero molto inferiore di consonanze intonate.

Tutte queste scale hanno tuttavia in comune un grosso limite: la scarsa possibilità di modulazione e trasposizione. Anche considerando le suddivisioni delle scale giuste sono pochissime le tonalità su cui è possibile suonare senza imbattersi in seri problemi con consonanze fuori tono. I rapporti fra le note sono infatti calcolati in relazione alla prima fondamentale. Se consideriamo come fondamentale un'altra nota cambiano di conseguenza tutti i rapporti. Questo avviene soprattutto se la nuova fondamentale è diversa dalla quarta o quinta. In definitiva occorrerebbe riaccordare lo strumento per la nuova tonalità. L'evoluzione della musica tonale esigeva a questo punto una soluzione. Un primo tentativo empirico è stato quello di duplicare i tasti delle note alterate (ovvero i cinque tasti neri) sugli strumenti a tastiera tipo organo o clavicembalo. In questo modo era possibile intonarli differentemente per adattarli ad altre tonalità, in genere quelle vicine. La vera soluzione però è arrivata con l'introduzione della scala temperata o temperamento equabile (vedi sezione successiva).

La scala temperata
Come abbiamo visto le note ricavate con le scale di giusta intonazione sono 12, considerando una volta sola le note enarmoniche. Sette sono quelle della scala maggiore, le altre cinque suddividono i toni interi. Il passo successivo è stato quello di suddividere l'ottava in dodici parti esattamente uguali ed ottenere 12 note equidistanti l'una dall'altra, eliminando di conseguenza le differenze fra le note enarmoniche (ad esempio Sol# e Lab diventano identiche). Il rapporto fra una nota e quella precedente è perciò sempre lo stesso ed è rappresentato dalla radice dodicesima di due (1,0595). Ogni parte della suddivisione è propriamente chiamata semitono temperato. Il tono è formato da due semitoni, è stata quindi eliminata anche la differenza fra tono grande e tono piccolo esistente nella scala giusta. Per valutare le piccole differenze di intonazione è stata introdotta una suddivisione più piccola chiamata cent, il quale corrisponde ad un centesimo di semitono. La formula per calcolare il valore di un intervallo in cent avendo il valore del rapporto è la seguente:

cent = log R * 1200 / log 2

Dove R è il valore del rapporto. Nel caso della quinta giusta, ad esempio, tale rapporto è 3/2, ovvero 1,5. La tabella 3 riporta gli intervalli di base giusti e temperati, con i relativi valori in cent.

Tabella 3: Valori in cent degli intervalli di base giusti e temperati.

Con i 12 semitoni tutti uguali la scala temperata permette qualsiasi trasposizione e modulazione utilizzando accordature fisse. Questa soluzione è tuttavia un compromesso con la scala giusta in quanto le note sono tutte leggermente stonate o, se preferite, adattate rispetto agli armonici naturali. Le tabelle 4 e 5 riportano tutti i valori in cent dei vari intervalli. Tali tabelle permettono di confrontare la scala giusta maggiore e minore con le relative temperate, evidenziando le differenze di intonazione in cent. Nella figura 6 è invece riportato un confronto grafico fra le medesime scale.

Calcolare il valore in cent è molto utile per diverse ragioni. Permette ad esempio un confronto diretto con la scala temperata, molto più di quanto lo permette una frazione numerica od un rapporto con i decimali. Inoltre, essendo il cent una misura logaritmica, è possibile calcolare un intervallo intermedio semplicemente sottraendo o sommando i valori di riferimento. Cosa meno immediata nel caso dei valori di rapporto i quali, come già visto, vanno calcolati con operazioni di divisione o moltiplicazione. Nel caso ad esempio dell'intervallo Re-La della scala maggiore giusta il rapporto è: 5/3: 9/8 = 40/27 (figura 4). Per calcolare invece il valore in cent di tale intervallo è sufficiente sottrarre i valori in cent delle note interessate (vedi tabella 4): 884 – 204 = 680 cent (calante di 20 cent rispetto alla quinta giusta temperata).

Tabella 4: Scale maggiori. Sulla prima colonna sono riportate le note in tonalità di Do. Sulla seconda la denominazione dell'intervallo. Successivamente abbiamo in ordine i rapporti delle frequenze e corrispondenza in cent relativi alla scala giusta ed alla scala temperata. Nell'ultima colonna è riportata la differenza in cent fra le due scale.

Tabella 5: Scale minori. Vedi note tabella 4.

Figura 6: Confronto scale giuste con scala temperata. Nella parte superiore è riportata la suddivisione della scala maggiore giusta. Nella parte inferiore quella della scala minore giusta. Nella parte centrale sono invece riportati i 12 semitoni della scala temperata. Gli scostamenti fra le varie scale sono visualizzati nella giusta proporzione.

Le consonanze perfette, quarta e quinta giusta, sono fuori tono di 2 cent, una differenza trascurabile per l'orecchio. Il primo intervallo a soffrirne è la terza maggiore, la quale nella scala temperata è più alta di 14 cent. Una tale differenza è infatti percepibile dall'orecchio ed è applicata ad un intervallo che, come sappiamo, è considerato basilare per la costruzione degli accordi. Questa è la ragione principale per cui inizialmente tale innovazione aveva i suoi detrattori. Tuttavia il battesimo ufficiale della scala temperata è stato ad opera di Bach nel 1722 con l'opera "Il clavicembalo ben temperato", uno dei suoi capolavori. L'opera raccoglie una serie preludi e fughe in tutte le dodici tonalità maggiori ed altrettante minori, per un totale di 24. L'intenzione di Bach era quella di sfruttare tutti i vantaggi di questo nuovo sistema musicale, senza limiti di trasposizioni e cambi di tonalità. Da questa opera in poi il nuovo sistema ha iniziato ad imporsi sempre di più in sostituzione alla scala giusta, fino a diventare lo standard della musica occidentale tutt'ora utilizzato. A questo punto è naturale porsi una domanda: quanto ne soffre la tonalità (ed in generale la musica) rinunciando ad avere gli intervalli giusti in favore di un sistema che permette completa trasponibilità? Secondo alcuni teorici le "stonature" introdotte dal sistema temperato rientrano nei limiti della tollerabilità. Questo anche perché non sono in misura superiore delle normali stonature introdotte dagli esecutori con strumento senza accordatura prestabilita (ad esempio i cantanti e gli strumenti ad arco). Altri invece hanno accolto il nuovo sistema esaltando il fatto che queste piccole stonature creano più movimento e vitalità negli accordi. In ogni caso oltre due secoli di musica fatta con questo sistema sono già una risposta.

La scala temperata, che è nata come un compromesso sulle scale di giusta intonazione, nel corso degli anni si è avviata a diventare una scala fine a stessa (vedi ad esempio la composizione delle scale, sezione "Tabella delle scale di base"). Nel XX secolo sono state sviluppate nuove forme musicali completamente scollegate dal sistema tonale. La dodecafonia ad esempio utilizza la scala di 12 suoni attribuendo ad ognuno la stessa importanza, senza cioè un preciso centro tonale. In queste forme musicali gli aggettivi consonante e dissonante perdono il significato che gli è stato attribuito in origine.

Confronto fra armonici e scala temperata
Come abbiamo visto gli armonici coinvolti nella costruzione delle scale sono i primi sei. Per quanto riguarda invece il contenuto timbrico del suono sono influenti tutti gli armonici che rientrano nella soglia di udibilità. In ogni caso è interessante esaminare la disposizione dei primi 31 armonici confrontandoli con la scala temperata. Essi sono riportati nel grafico di figura 7. Il grafico è in scala logaritmica, come del resto tutte le rappresentazioni dell'ottava fatte in questo libro. La scala logaritmica risulta particolarmente comoda in quanto è rapportabile alla percezione uditiva. Permette cioè di visualizzare uguali rapporti in uguali lunghezze, In altre parole la lunghezza in scala di un preciso intervallo è identica in tutte le ottave. I rapporti fra le frequenze rimangono infatti gli stessi mentre questo non avviene se calcoliamo le differenze. Gli armonici invece sono multipli interi di una frequenza di base, sono perciò tutti equidistanti l'uno dall'altro di quella precisa frequenza. La loro rappresentazione logaritmica è per questo motivo sempre più stretta man mano che si alza la loro frequenza. Il cent è una unità di misura logaritmica perciò, in un grafico di questo tipo, i valori sono visualizzati in modo lineare.

In figura 7 gli armonici sono raffigurati dalle linee continue orizzontali, al di sopra delle quali è riportato il relativo numero progressivo (dal 1° al 31°). Essi sono disposti, nella giusta proporzione, su una griglia di 12 righe e 5 colonne. Le righe sono i 12 semitoni della scala temperata su cui è possibile comparare gli armonici. Fuori dalla griglia, a sinistra, sono riportate come riferimento le note in tonalità di Do ed i valori in cent dei semitoni della scala temperata. A destra della griglia sono invece riportati i valori in cent degli armonici. Tale valore è posizionato in linea con gli armonici stessi. Le colonne sono le 5 ottave su cui si distribuiscono gli armonici. La colonna più a sinistra è la prima ottava, l'ultima a destra è la quinta ottava.

Con questo grafico è possibile fare alcune interessanti valutazioni. In ogni ottava sono presenti il doppio degli armonici dell'ottava precedente. Inoltre tutti gli armonici presenti in una ottava si ripetono nell'ottava successiva, insieme ad altrettanti armonici nuovi intermedi. Altra particolarità sta nel fatto che la progressione degli armonici 16°, 17°, 18° e 19° è pressoché equivalente alla scala cromatica temperata.

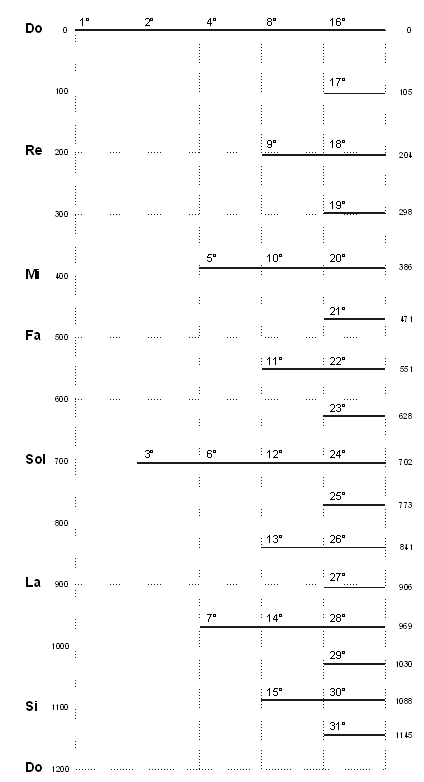
Figura 7: Disposizione dei primi 31 armonici in riferimento all'ottava musicale temperata.

La tonalità e le cadenze
Approfondiamo a questo punto uno dei concetti basilari della musica occidentale di ieri e di oggi, la tonalità. Per tonalità si intende un modo di fare musica che considera i suoni in relazione fra di loro, come se fossero attratti da un centro gravitazionale detto tonica. Le scale sono state originate in base a questo principio, abbiamo infatti visto come la tonica è anche la radice da cui vengono originate le altre note. Tuttavia non è sufficiente l'uso indiscriminato della scala maggiore e relativi accordi per ottenere questo risultato. Alcune tonalità sono molto affini fra loro ed è necessario disporre di mezzi che permettono di differenziarle. Questi mezzi sono delle successioni di accordi chiamate cadenze. Le cadenze sono utilizzate anche per definire la chiusura di un periodo musicale o dell'intero brano. Esistono vari tipi di cadenze, qui analizzeremo solo quelle che hanno la funzione di affermare la tonalità.

Supponendo per comodità di essere in tonalità di Do maggiore le tonalità più affini sono:

• La relativa minore (La minore), perchè contiene le stesse note.
• La parallela minore (Do minore), perchè ha la stessa tonica.
• Le tonalità vicine ovvero quelle differenziate da una sola alterazione in chiave (Fa maggiore con un bemolle, Sol maggiore con un diesis, vedi sezione 3.4.7), perchè la differenza è minima.

La relativa minore è facilmente differenziabile utilizzando le cadenze in tonalità minore, esse sono analizzate di seguito. La parallela minore si distingue soprattutto perché ha pochi accordi in comune con la tonalità maggiore. In ogni caso le cadenze in tonalità minore le tratteremo dopo aver analizzato quelle in tonalità maggiore.

Le tonalità vicine sono le più "ambigue" in quanto hanno molti accordi in comune. Il modo per distinguerle è quello di far sentire i gradi che differenziano tali tonalità, vediamo in che modo. La scala di Do maggiore non presenta note alterate. Nelle tonalità vicine, ovvero Fa maggiore e Sol maggiore, abbiamo le seguenti alterazioni: Sib nella prima e Fa# nella seconda (vedi sezione "Il circolo delle quinte"). Da questo ragionamento risulta chiaro che le note Si e Fa (senza alterazioni) stabiliscono in modo inequivocabile che siamo in tonalità di Do maggiore. In tale tonalità gli accordi che contengono il Si sono: Si dim, Mi m e Sol. Quelli che contengono il Fa sono: Fa, Si dim e Re m. Infine gli accordi che contengono entrambe le note sono: Si dim e Sol 7 (vedi tabelle 2 e 4 in "Teoria generale: Gli Accordi"). Nelle cadenze viene fatto uso di questi accordi. La dominante, in questo caso il Sol, è l'accordo privilegiato, nel senso che spesso è sufficiente la sequenza Sol-Do per affermare la tonalità. Questo avviene perché il movimento della fondamentale di una quinta discendente o quarta ascendente (come appunto nel caso di Sol-Do) è un movimento che risolve in modo naturale. Per capire questo concetto confrontiamo gli armonici del Do con quelli del Sol riportati in tabella 6, considerando il Do più basso con frequenza 1.

Tabella 6: Primi dieci armonici di Do e Sol.

La nota corrispondente al secondo armonico, Do´, contiene tutti gli armonici del Do che sono multipli di due. Come abbiamo già potuto constatare, da questa affinità è derivato l'intervallo primario, l'ottava.

Esaminiamo ora gli armonici del Sol, nota corrispondente al terzo armonico abbassato di un'ottava. Quelli in posizione pari (2°, 4°, 6°, ecc.) sono anche nel Do. Quelli dispari (1°, 3°, 5°, ecc.) sono anch'essi presenti nel Do ma un'ottava sopra. Il Sol contiene perciò tutti gli armonici del Do che sono multipli di tre, ma su ottave differenti. Se infine esaminiamo il Sol´, identico cioè al terzo armonico, esso contiene tutti gli armonici del Do multipli di tre sulla medesima ottava. La conseguenza di queste affinità è che il Sol può essere considerato come un Do senza il primo armonico. Il Do è quindi sott'inteso nel Sol ed è considerato la sua risoluzione naturale. Ricordare a questo proposito il concetto di altezza virtuale trattato nella parte finale della sezione 3.4.1. E' possibile fare un ragionamento analogo anche per le note derivate dagli armonici successivi, ma l'affinità diventa sempre più lontana ed inavvertibile.

Questa sequenza di accordi, dominante-tonica, corrispondente ad un intervallo di quinta discendente, è chiamata cadenza autentica o perfetta. Nel caso di Do maggiore tale sequenza è appunto: Sol-Do. L'accordo di dominante ha perciò due importanti caratteristiche per affermare la tonalità: contiene la nota Si e permette il movimento dalla fondamentale di una quinta sotto. Come abbiamo visto, oltre al Si è necessario utilizzare anche il Fa per eliminare ogni dubbio sulla tonalità. Se aggiungiamo il Fa all'accordo di Sol otteniamo l'accordo di settima di dominante, il Sol 7. L'esempio musicale di figura 8 riporta la successione Sol 7 – Do:

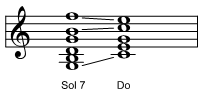
Figura 8: Sequenza accordi Sol 7 - Do eseguita sulla chitarra con accordi aperti.

L'accordo di settima di dominante contiene il tritono (quinta diminuita) con le note Si-Fa, che è l'intervallo dissonante per eccellenza. In questo passaggio la dissonanza viene risolta in una terza maggiore (consonanza, situazione di riposo) utilizzando le note adiacenti al tritono stesso: il Si passa a Do ed il Fa passa a Mi. Inoltre si presenta anche il passaggio della fondamentale di una quarta sopra. Tali passaggi sono evidenziati in figura 8 dalle linee di collegamento trasversali. Nella musica tonale è molto frequente la risoluzione delle dissonanze nelle note strettamente adiacenti, ovvero un semitono sopra o sotto. Inoltre la risoluzione della dissonanza in una situazione di riposo sull'accordo di tonica, contribuisce a rendere la cadenza ancora più incisiva.

Il tritono ha perciò una funzione basilare nell'armonia tonale. In ogni scala maggiore tale intervallo si presenta una volta sola (fra il quarto ed il settimo grado) e stabilisce perciò una precisa tonalità. In conclusione gli accordi di dominante utilizzati in modo cadenzale possono contenere la settima.

Il Sol 7 può essere inteso come un Si dim con basso in Sol. Il Si dim può perciò assolvere alla stessa funzione, anche se in modo meno efficace.

Nella cadenza perfetta si utilizza un passaggio di due accordi. In certi casi è necessario utilizzare una cadenza più lunga per affermare la tonalità in modo più deciso. Si tratta della cadenza composta. Essa equivale ad una cadenza perfetta preceduta da un altro accordo, per l'esattezza un accordo contenente la nota Fa. Se escludiamo il Si dim (che come abbiamo visto la sua funzione è già assolta dal Sol 7) rimangono il Fa ed il Re m, ovvero il quarto ed il secondo grado. Abbiamo perciò due cadenze composte: IV-V-I (Fa – Sol - Do) e IIm-V-I (Re m – Sol – Do). Anche nella cadenza composta il quinto grado può contenere la settima di dominante. Nel primo caso (IV-V-I) la cadenza contiene tutti accordi maggiori ed il basso compie un salto di seconda ascendente e quarta ascendente. Nel secondo caso (IIm-V-I) il basso compie un duplice salto di quarta ascendente, cosa che rende il passaggio particolarmente incisivo. Quest'ultima cadenza è utilizzata moltissimo, in modo particolare nel jazz, dove viene spesso eseguita con gli accordi estesi. In tonalità di Do maggiore tali accordi sono: Re m7 – Sol 7 – Do maj7.

Se in una cadenza sostituiamo l'accordo finale di tonica con un altro, abbiamo una cadenza evitata. Tipico è l'utilizzo di questa cadenza per armonizzare la frase melodica finale di un brano, la quale veniva poi ripetuta identica ma con la cadenza perfetta. In questo modo si rendeva il finale più forte ed incisivo. La cadenza evitata viene tuttavia utilizzata anche in altre maniere, ad esempio sostituendo l'accordo di tonica con un altro modulante, che porta cioè ad un'altra tonalità. Quello che ci interessa è il caso in cui la tonalità rimane la stessa. L'accordo da utilizzare nella sostituzione è molto legato alla nota con cui si chiude la melodia. La nota finale in genere fa anche parte dell'accordo di tonica, in tonalità di Do maggiore essa può essere Do, Mi o Sol. L'accordo sostituto dovrà contenere tale nota e dovrà essere diverso da Do (accordo di tonica) e Sol (il Sol rimane sempre l'accordo che precede la chiusura). Se ad esempio la melodia chiude con la nota Do possiamo utilizzare gli accordi Fa o La m. Se chiude con la nota Mi possiamo utilizzare gli accordi Mi m o La m. Se infine chiude con la nota Sol possiamo utilizzare solo l'accordo Mi m. Esistono tuttavia molte eccezioni.

Un altro tipo di cadenza è la cadenza plagale, essa corrisponde al passaggio IV-I (sottodominante-tonica, Fa-Do). In realtà questa cadenza non basta ad affermare la tonalità. Per ottenere questo risultato può servire ad esempio far precedere la dominante alla cadenza (V-IV-I), ottenendo così una successione molto simile alla cadenza composta. Nella cadenza plagale l'accordo di sottodominante può anche essere minore: IVm-I. Vediamo cosa comporta questa modifica nell'esempio musicale in tonalità di Do maggiore riportato in figura 9:

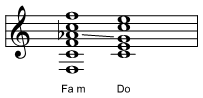
Figura 9: Sequenza accordi Fa m - Do eseguita sulla chitarra nelle posizioni più vicine alla paletta.

Il Fa m contiene la nota Lab, la quale non è presente nella scala di Do maggiore. Questo contribuisce a creare una tensione armonica che si risolve facendo scendere la nota di un semitono: Lab → Sol (vedi linea di collegamento in figura 9). Viene perciò utilizzata una nota che non è nella scala per rendere il passaggio più incisivo.

La tabella 7 riepiloga tutte le cadenze descritte nella presente sezione.

Tabella 7: Tipi cadenze

Nel caso di tonalità minori le cadenze devono rimanere inalterate, questo ovviamente per mantenere la stessa efficacia. Cambia solo l'accordo di tonica che in questo caso sarà minore. La cadenza perfetta diventerà perciò V-Im e quella composta IIm-V-Im o IV-V-Im. Anche nelle cadenze in tonalità minore è possibile utilizzate la settima sull'accordo di dominante. Le cadenze in tonalità minore comportano alcune conseguenze armoniche molto interessanti. Consideriamo, ad esempio, la tonalità di Do minore. Se armonizziamo la scala avremo gli accordi riportati in tabella 8:

Tabella 8: Armonizzazione scala di Do minore naturale.

La regola sulle cadenze contrasta con gli accordi dell'armonizzazione. La cadenza prevede ad esempio un Sol maggiore mentre nell'armonizzazione è minore. Questo ovviamente è derivato dal fatto che gli accordi delle cadenze provengono da una scala maggiore, non minore. L'accordo di Sol maggiore contiene il Si (sensibile) anziché il Sib, opera cioè un'alterazione sul settimo grado della scala minore. Il risultato è la scala minore armonica. Se a questo punto utilizziamo la cadenza composta introducendo anche il Fa maggiore o Re minore, occorre operare un'altra alterazione in quanto entrambi gli accordi contengono il La (sesta maggiore) anziché il Lab. Otteniamo a questo punto anche la scala minore melodica. Le scale minore armonica e melodica (trattate nelle sezioni "La scala minore melodica" e successivamente) sono perciò derivate da una esigenza ben precisa, quella di utilizzare le cadenze fondamentali per affermare la tonalità. Di conseguenza la modalità di utilizzo di queste due scale, in sostituzione alla scala minore naturale, è strettamente legata al fatto di essere o meno in una situazione cadenzale. Oltre a questo sono state anche introdotte alcune regole, giustificate spesso da ragioni melodiche o di chiarezza. Nell'armonia classica ad esempio la scala minore melodica veniva utilizzata solo nel modo ascendente, nel modo discendente si utilizzava la scala minore naturale. Questo per mantenere chiara la sensazione di tonalità minore.

Il circolo delle quinte
Il circolo delle quinte rappresenta le affinità fra le tonalità distanti intervalli di quinta giusta. La tonalità viene convenzionalmente riferita alla prima nota della scala maggiore se il brano è in tonalità maggiore, o della scala minore naturale se il brano è in tonalità minore. Gli intervalli della scala maggiore sono strutturati in modo tale che eseguendo trasposizioni della tonalità una quinta sopra deve sempre essere alzata una nota di un semitono, per mantenere la stessa si.. Se al contrario eseguiamo trasposizioni una quinta sotto deve essere abbassata una nota di un semitono. Osserviamo come esempio le seguenti trasposizioni della scala maggiore:

Scala di riferimento, Do maggiore:

Scala di Sol maggiore, un diesis:

Scala di Re maggiore, due diesis:

Scala di Fa maggiore, un bemolle:

Scala di Sib maggiore, due bemolle:

La tonalità di Do maggiore non ha note alterate. Se trasportiamo la tonalità una quinta sopra abbiamo la scala di Sol maggiore. Questa scala contiene un diesis (Fa#). Se la trasportiamo un'altra quinta sopra abbiamo il Re maggiore che contiene due diesis, quello di prima più uno nuovo (Fa# e Do#), eccetera. Se al contrario trasportiamo la tonalità una quinta sotto (sempre a partire dal Do maggiore) abbiamo la scala di Fa maggiore che contiene un bemolle (Sib). Un'altra quinta sotto abbiamo il Sib maggiore che contiene due bemolle, anche in questo caso l'alterazione di prima più una nuova (Sib e Mib). Se continuiamo ad applicare lo stesso procedimento per tutte le tonalità rimanenti otteniamo il cosiddetto circolo delle quinte, rappresentato in figura 10.

Il circolo delle quinte va letto in questo modo. Il Do è la nota di partenza. Girando in senso orario abbiamo le quinte ascendenti, le note relative sono riportate all'esterno del cerchio. Al contrario, girando in senso antiorario, abbiamo le quinte discendenti, le note relative sono riportate all'interno del cerchio. Nel cerchio più piccolo sono riportate le tonalità relative minori. Nello spazio fra i due cerchi sono riportati i diesis progressivi fino a sette. Nel cerchio interno sono riportati i bemolle progressivi sempre fino a sette. Tre tonalità maggiori si sovrappongono: Si, Fa# e Do# sono le rispettive omofone di Dob, Solb e Reb. Applicando al Do dodici quinte consecutive, ascendenti o discendenti, abbiamo un altro Do, il cerchio perciò si chiude evidenziando tutte le dodici tonalità possibili.

Nella figura 10 in basso sono riportati gli esempi di come vengono trascritte le tonalità su pentagramma. I diesis o bemolle vengono riportati all'inizio di ogni rigo nello stesso ordine derivato dal circolo delle quinte, i quali prendono il nome di alterazioni in chiave. Queste alterazioni indicano (salvo diversa specificazione) che tali note devono essere alzate o abbassate di un semitono durante l'esecuzione del brano. Gli esempi su pentagramma sono due, il primo è relativo alle tonalità con i diesis, il secondo alle tonalità con i bemolle. Al di sotto di ogni raffigurazione è riportato il nome della tonalità sia maggiore che minore. La riga relativa alla progressione riporta le sette note alterate nel rispettivo ordine. Se ad esempio abbiamo 4 diesis in chiave, la tonalità è Mi maggiore o Do# minore. I diesis vanno indicati in ordine sulle note: Fa, Do, Sol, Re. Durante l'esecuzione del brano queste 4 note vanno alzate di un semitono.

Figura 10: Circolo delle quinte.

Le tonalità vengono trascritte in questa maniera perché la notazione musicale è stata basata sulla scala di Do maggiore. Se le alterazioni non venissero riportate solo all'inizio, le tonalità diverse da Do maggiore necessiterebbero alterazioni ripetute nel corso del brano, rendendo la lettura più difficile.

Il circolo delle quinte evidenzia una cosa molto importante, la distanza fra le tonalità. Due tonalità sono dette vicine quando hanno solo una alterazione in chiave come differenza. Con l'aumentare delle alterazioni le tonalità si allontanano. Le tonalità vicine sono perciò quelle collocate una quinta sopra o sotto, come avviene nel circolo delle quinte. La tonalità più lontana è quella collocata dalla parte opposta del cerchio, la quale dista una quinta diminuita. Il cambio di tonalità nel corso di un brano tonale prende il nome di modulazione. La sensazione derivata da una modulazione è in genere quella di un cambio di umore all'interno del brano. Tale mutamento è condizionato dai seguenti fattori principali:

• Distanza fra le tonalità.
• Passaggio da modo maggiore a minore o viceversa.
• Modulazione brusca o morbida. Nel primo caso si passa direttamente da una tonalità all'altra. Nel secondo vengono utilizzati accordi di passaggio o preparatori (in genere comuni ad entrambe le tonalità) seguiti da accordi cadenzali per affermare la nuova tonalità (vedi sezione "La tonalità e le cadenze").

Vi rimando ad un trattato di armonia per un eventuale approfondimento sulle regole utilizzate per modulare nei vari generi musicali.

Video Blue Moon - Ahmad Jamal http://itunes.apple.com/fr/album/blue-moon/id496348341Blue Moon is not just Ahmad Jamal's latest album, it's his latest masterpiece, suffused with a f... inserito il 05/12/2011  da - visualizzazioni: 7521

Jazz Istruzioni per l'uso roberto gatto ... inserito il 14/05/2008  da esomare - visualizzazioni: 8877

© 2007, 2008 - Paolo Guiducci - Se sei interessato alla pubblicazione contattare l'autore: http://pguiducci.com - Tutti i diritti riservati

Questa pagina è stata visitata 33.221 volte Data pubblicazione: 24/06/2008 Home |  Articoli |  Comunicati |  Io C'ero |  Recensioni |  Eventi |  Lezioni |  Gallery |  Annunci Artisti |  Saranno Famosi |  Newsletter |  Forum |  Cerca |  Links | Sondaggio |  Cont@tti