INDICE LEZIONI

Dipingere con la voce La forza di legame di Sandra Evangelisti evasama@tin.it

La lezione scorsa abbiamo parlato di legami covalenti e di legami ionici e abbiamo detto che mentre i primi permettono la formazione di molecole, i secondi fanno si che gli atomi si uniscano tra di loro a formare aggregati cristallini.
Le molecole, a loro volta, possono "legarsi" a formare strutture sempre più complesse fino ad arrivare a quelle "macrostrutture" che ritroviamo nel mondo che ci circonda.
A seconda del tipo di legame che tiene uniti i diversi elementi parleremo di materia allo stato solido, allo stato liquido e allo stato gassoso o aeriforme.
Esiste, in realtà, anche un quarto stato di aggregazione in cui la materia è costituita da nuclei atomici ed elettroni liberi.
Parliamo in questo caso dello stato di plasma ⁽¹⁾.

In un solido, gli atomi, gli ioni o le molecole che lo costituiscono sono tenuti insieme da forze di legame piuttosto intense.
Tali particelle non hanno libertà di muoversi all'interno della struttura e "vibrano intorno a posizioni fisse" ⁽²⁾.
Il solido ha una sua forma ben definita e può essere afferrato.
Dando energia, sotto forma di calore, ad un solido la velocità di vibrazione molecolare aumenta, le forze di legame si indeboliscono e le molecole sono in grado di errare "attraverso la sostanza vibrando in posizioni non-fisse" ⁽³⁾.
Si ha così la fusione, il passaggio, cioè, da solido a liquido.

"In un liquido, le molecole sono meno vincolate rispetto ad un solido e possono muoversi con maggiore libertà".

Risentendo della forza di gravitazione terrestre, la sostanza che non ha più una forma fissa tende ad assumere la forma del recipiente che la contiene ⁽⁴⁾.
"Se la sostanza riceve ulteriore energia le molecole da cui è formata vibrano con velocità ancora più alte" ⁽⁵⁾.

Liberatesi dalle forze elettrostatiche che le tenevano vincolate all'interno del liquido, le molecole si diffondono nell'ambiente circostante espandendosi "fino a riempire tutto lo spazio disponibile" ⁽⁶⁾.

Tale fenomeno viene definito vaporizzazione e il nuovo stato in cui la sostanza si trova viene definito "stato gassoso o aeriforme".
"Il modo in cui una sostanza si presenta in natura" il modo, cioè, in cui sono "aggregati" tra di loro gli elementi che la costituiscono, è influenzato in modo significativo "dalle condizioni esterne a cui la sostanza è stata sottoposta al momento della sua formazione oppure a cui è sottoposta nel momento in cui la stiamo osservando".

Tra queste condizioni svolgono un ruolo importante la pressione e la temperatura ⁽⁷⁾.

MA PROCEDIAMO CON ORDINE…

"Per forza di legame s'intende la forza che tiene uniti due atomi" ⁽⁸⁾.

Nelle ultime due lezioni abbiamo parlato di come la forza di legame dipenda non soltanto dal grado di elettronegatività di un singolo atomo, cioè dalla sua capacità di "attirare gli elettroni all'interno di un legame", quanto anche dal tipo di legame che si viene a formare.

"La forza di legame è misurata dalla quantità di energia che deve essere fornita per rompere il legame" ⁽⁹⁾, cioè, dall'energia necessaria per spezzare un legame e "riottenere gli atomi liberi".

La quantità di energia che "bisogna fornire per rompere un legame" è uguale a quella che "si libera quando lo stesso legame viene costituito" ⁽¹⁰⁾.
L'energia di un legame può essere definita, infatti, anche come quella quantità di energia "guadagnata dall'ambiente" quando si forma un legame ⁽¹¹⁾.
Più sono forti i legami, dunque, e maggiore sarà l'energia di legame necessaria per ottenerne la rottura.

"Un modo per immettere energia in un sistema è quello di aumentare la sua temperatura, cioè, di conferire alle molecole una maggiore energia cinetica".

Questo ulteriore apporto di energia cinetica, aumentando il movimento delle molecole, può determinare, se questi "moti molecolari sono sufficientemente violenti", la rottura di legami chimici preesistenti e, allo stesso tempo, la formazione di legami nuovi ⁽¹²⁾.

Sia i legami covalenti che quelli ionici rientrano nella categoria dei legami forti.
"La formazione e la rottura di legami covalenti" sono, infatti, fenomeni di natura violenta ⁽¹³⁾.

I legami ionici, invece, per quanto rientrino anch'essi nella categoria dei legami forti, richiedono, come vedremo in seguito, una minore energia di legame per essere scissi.

Abbiamo detto che, allo stato solido, "le particelle elementari" sono disposte le une accanto alle altre in modo "più o meno ordinato" ⁽¹⁴⁾.
Come conseguenza di questo "modo più o meno ordinato" in cui le varie particelle si distribuiscono all'interno della materia si vengono a formare figure geometriche dalla forma caratteristica.
Tali figure si ripetono, all'interno del solido, "svariate volte" ed in modo piuttosto regolare ⁽¹⁵⁾.

"Nei solidi, dunque, la distribuzione spaziale dei punti di equilibrio segue generalmente uno schema geometrico particolare".
A tale schema geometrico viene dato il nome di "reticolo cristallino" ⁽¹⁶⁾.
Cominciamo col dire che con il termine reticolo ci si riferisce alla "sequenza periodica di punti nello spazio che lo riempiono senza lasciare vuoti" ⁽¹⁷⁾.
Definiamo, invece, base "ogni gruppo di atomi che si ripete con la sequenza periodica del reticolo".
Reticolo + base = struttura ⁽¹⁸⁾.

Quindi una "struttura cristallina" è una struttura costituita da "unità" di base semplici dette anche "celle elementari" che, "ripetute nello spazio formano l'intero reticolo" ⁽¹⁹⁾.

Ognuna di queste "unità di base" è, a sua volta, caratterizzata da un "perfetto" ⁽²⁰⁾ ordine in cui ogni particella si trova ai "vertici di figure geometriche tridimensionali ben definite" ⁽²¹⁾.
Questi tipi di solidi prendono il nome di "solidi cristallini".
La maggior parte dei composti "a livello macroscopico", che osserviamo intorno a noi, hanno come struttura di base una struttura di tipo cristallino ⁽²²⁾.

Ma non tutti i solidi sono cristallini: esiste una categoria di solidi che, nonostante nel "comportamento sia simile ai solidi cristallini", se ne differenzia in quanto la "distribuzione spaziale dei punti di equilibrio non è geometrica" ma irregolare.

In questa categoria di solidi gli elementi non vanno a strutturarsi in un reticolo cristallino ma si distribuiscono in modo disordinato all'interno della sostanza ⁽²³⁾. Tali sostanze prendono il nome di solidi amorfi ⁽²⁴⁾.
Tuttavia, essendo un solido amorfo, date le sue caratteristiche strutturali, assimilabile molto di più alla categoria dei "liquidi molto viscosi" anziché a quella dei "solidi cristallini" ⁽²⁵⁾, ritengo opportuno rimandare il discorso sui solidi amorfi alla prossima lezione quando parleremo, appunto, delle proprietà e della dinamica dei liquidi.

Ad ogni modo, sia che si tratti di un solido cristallino o che si tratti di un solido amorfo, ogni atomo, ione o molecola che lo costituisce è "mantenuto al proprio posto" da legami, più o meno forti, attivi tra le particelle vicine ⁽²⁶⁾.
Pertanto esse "oscillano intorno ad un punto fisso" (27) e "possono subire solo piccolissimi spostamenti attorno a posizioni di equilibrio ben determinate" ⁽²⁸⁾.
Gli atomi e le molecole non sono, dunque, in grado di muoversi liberamente all'interno della sostanza come, invece, abbiamo detto accade nel caso dei liquidi e dei gas ⁽²⁹⁾.
Per tale motivo un corpo allo stato solido si presenta con un volume proprio e una forma geometrica definita ⁽³⁰⁾.
Avendo ogni solido dimensione e forma costante è possibile afferrarli a differenza di quanto, invece, avviene nel caso di una sostanza allo stato liquido o di una sostanza allo stato aeriforme ⁽³¹⁾.

Le forze che tengono uniti i vari elementi all'interno dei solidi cristallini sono di diversa natura.
Oltre ai legami covalenti e ionici, di cui abbiamo parlato in modo dettagliato nella lezione scorsa esistono altri tipi di legami tra cui il legame metallico, di cui parleremo tra breve, e i cosiddetti legami deboli, come il legame a idrogeno e le forze di Van der Waals. Di questi ultimi due legami, che solitamente sono attivi a livello intramolecolare, invece, mi propongo di parlarne, in modo più approfondito, nelle prossime lezioni.
A seconda del tipo di legame che tiene unite le particelle tra di loro, i solidi cristallini possono essere classificati in solidi covalenti, soldi ionici, solidi metallici e in solidi molecolari. "Nelle situazioni reali" è molto più probabile, tuttavia, trovare solidi caratterizzati dalla compresenza di legami di diversa natura ⁽³²⁾. A quest'ultima categoria di solidi viene dato il nome di solidi ibridi.

Un discorso a parte va fatto per i solidi amorfi. Ma, come ho già detto, preferisco rimandare l'argomento alla prossima lezione quando tratteremo delle sostanze allo stato liquido.

Tuttavia, prima di passare ad una descrizione più particolareggiata di questi differenti tipi di solidi cristallini, ritengo sia necessario fare una piccola digressione per parlare del legame metallico.

Iniziamo col dire che si definiscono metalli tutti quegli elementi della tavola periodica che, in una interazione, hanno la "tendenza a cedere i loro pochi elettroni di valenza e a trasformarsi in cationi" ⁽³³⁾.
Questi cationi vanno, poi, a distribuirsi, all'interno dello "spazio tridimensionale" ⁽³⁴⁾, secondo uno schema geometrico ben definito.
Gli elettroni di valenza "ceduti" dagli atomi che costituiscono il solido metallico, vanno, a loro volta, a formare "un mare di elettroni liberi" che si muove uniformemente in tutto il cristallo ⁽³⁵⁾.

"L'attrazione che si instaura tra i cationi formatisi dagli atomi metallici e la nuvola di elettroni ‘delocalizzati' in cui questi sono immersi costituisce il legame metallico" ⁽³⁶⁾.
Tale "comproprietà di elettroni" a cui si deve, quindi, "la coesione interna del metallo stesso" ⁽³⁷⁾, è anche "responsabile delle proprietà macroscopiche di questi elementi", tra cui, "la loro elevata conducibilità elettrica" ⁽³⁸⁾ e la loro "elevata" duttilità" ⁽³⁹⁾.
Gli elettroni liberi, infatti, possono spostarsi facilmente da un atomo all'altro e "scorrere attraverso il metallo trasportando calore o elettricità" ⁽⁴⁰⁾.
Della duttilità parleremo, in modo più dettagliato, più avanti.

Ritorniamo adesso a quanto stavamo dicendo a proposito delle differenze, a livello microscopico, che esistono tra i diversi solidi cristallini.
Cominciamo dai solidi covalenti.

Si definiscono solidi covalenti tutti quei solidi "in cui le particelle sono legate tra loro da legami omopolari o covalenti" ⁽⁴¹⁾.
Il legame covalente, come abbiamo detto, ha un'alta energia di legame ed è responsabile della formazione di solidi molto duri, indeformabili ed isolanti.
Il diamante è un tipico esempio di questa categoria di solidi ⁽⁴²⁾.

Nei solidi ionici, invece, "ai vertici del reticolo troviamo ioni positivi e negativi alternati gli uni agli altri". Esempio tipico il cristallo di sale ⁽⁴³⁾.
I legami ionici hanno energia di legame abbastanza alta e sono responsabili della formazione di solidi isolanti, indeformabili ma, allo stesso tempo fragili ⁽⁴⁴⁾.

Nei solidi metallici, come abbiamo appena visto, "ai vertici del reticolo cristallino sono posizionati ioni positivi immersi in una nube elettronica costituita dagli elettroni dell'ultimo strato" messi in comune dai diversi cationi che costituiscono il reticolo ⁽⁴⁵⁾.
Come conseguenza della presenza di questa "nuvola di elettroni liberi" il legame metallico ha un'energia di legame modesta.
I solidi metallici sono duttili e buoni conduttori sia di calore che di elettricità ⁽⁴⁶⁾.
Infine abbiamo i solidi molecolari, dove "ai vertici del reticolo troviamo molecole, legate tra loro da legami di natura elettrostatica".
Essi sono solidi molto teneri. Un esempio di questa categoria di solidi è il saccarosio ⁽⁴⁷⁾.

Nei solidi ibridi, in ultimo, gli atomi e le molecole sono tenuti insieme non da un unico legame, come nel caso dei solidi fino ad ora descritti, ma dalla compresenza di legami di tipo diverso ⁽⁴⁸⁾.

Abbiamo detto, inoltre, che, per quanto in un corpo solido, i vari elementi siano "mantenuti ai loro posti da legami più o meno forti attivi tra le particelle vicine" ⁽⁴⁹⁾, "in natura non esiste l'immobilità assoluta" per cui nei corpi allo stato solido gli atomi, gli ioni o le molecole "vibrano attorno a posizioni geometriche fisse" ⁽⁵⁰⁾.
Questo significa che se colpiamo un solido in un punto il movimento si trasmette a tutti gli altri atomi del reticolo e "l'intero reticolo vibra".
Tale colpo può essere di natura più o meno violenta.
Più il colpo è violento maggiore sarà la possibilità che nel punto in cui l'oggetto viene colpito si verifichi una rottura di legame tra gli atomi.
Questo accade, per esempio, "quando si frantuma una pietra o se ne fanno saltare dei pezzi" ⁽⁵¹⁾.
Per rompere una pietra particolarmente friabile ⁽⁵²⁾, ma lo stesso discorso vale per qualunque altro tipo di solido che sia fragile, non sarà necessario usare molta energia in quanto gli atomi che lo costituiscono sono tenuti insieme da forze di minore entità.

Se, invece, la pietra da frantumare è una pietra piuttosto resistente, allora sarà necessario un quantitativo maggiore di energia per rompere i legami che tengono uniti gli atomi tra di loro.
Ma che cosa significa dire che un corpo è più fragile o che un corpo è più resistente?
Iniziamo col puntualizzare che in natura esistono diversi tipi di "solidi".
Oltre alla "pietra", ad esempio, esistono i metalli, il legno, i sali etc.
Esistono, poi, altri tipi di materiali solidi "che derivano dalla lavorazione e trasformazione di materie prime di origine naturale" ⁽⁵³⁾ come nel caso dell'acciaio ⁽⁵⁴⁾, del cemento ⁽⁵⁵⁾ o della ceramica ⁽⁵⁶⁾.
Esistono, infine, ancora altri tipi di materiali allo stato solido che vengono sintetizzati dall'uomo all'interno dei laboratori come le materie plastiche ⁽⁵⁷⁾ o le fibre sintetiche ⁽⁵⁸⁾.

Ognuno di questi materiali presenta delle proprietà (59) "meccaniche" che lo distinguono dagli altri solidi, quali la "durezza", la "resistenza" e l' "elasticità" ⁽⁶⁰⁾.
Proprietà, queste, che determinano la maggiore o minore propensione di un corpo, rispettivamente, ad essere scalfito, a rompersi o ad essere deformato.
C'è da dire, inoltre, che all'interno di una stessa categoria di solidi ce ne possono essere, ad esempio, alcuni che sono più "resistenti" di altri.
Ci sono rocce, infatti, che richiedono "molta energia" per essere spaccate mentre ce ne sono altre, talmente fragili, che si sbriciolano semplicemente a toccarle.

Tutte queste proprietà "dipendono dalle forze che tengono insieme le particelle che li costituiscono" ⁽⁶¹⁾.

Stabilito questo, andiamo ad analizzare, in modo più approfondito, le diverse proprietà "meccaniche" che caratterizzano i vari tipi di solidi. Iniziamo con la durezza.

"La resistenza che un minerale oppone ad essere graffiato o alla scalfittura viene chiamata durezza" ⁽⁶²⁾.

La durezza dipende dalle forze di coesione presenti fra gli atomi ⁽⁶³⁾ e può essere determinata col sistema della graffiatura: non essendo possibile misurare con una certa attendibilità la durezza di un materiale si è deciso di ricorrere, ai fini sperimentali, ad una "scala empirica di dieci minerali campione disposti in ordine crescente di durezza" ⁽⁶⁴⁾. All'interno di questa scala ognuno dei "minerali campione" selezionati è in grado di scalfire "qualunque minerale con lo stesso valore o un valore più basso" ed essere, a sua volta, "scalfito da qualunque minerale con valore più alto" ⁽⁶⁵⁾.
Tale scala, conosciuta col nome di ‘scala di Mohs', dal suo ideatore ⁽⁶⁶⁾, il mineralogista Friedrich Mohs (1773-1839) ⁽⁶⁷⁾, fu costruita nel 1832 utilizzando una serie di punte ricavate da dieci minerali scelti fra i più comuni e facilmente reperibili ⁽⁶⁸⁾.
Segue l'elenco dei dieci minerali che costituiscono la scala di Mohs presentati in ordine di durezza crescente dall'1, il più tenero, "determinato dalla durezza del talco", al 10, "valore che determina la durezza massima di un minerale e che corrisponde al diamante" ⁽⁶⁹⁾:

1) talco (si rigano facilmente con l'unghia e sono untuosi al tatto);
2) gesso (si rigano con l'unghia);
3) calcite (si rigano con un filo di rame);
4) fluorite;
5) apatite (si rigano con un temperino);
6) feldspato (ortoclasio ⁽⁷⁰⁾);
7) quarzo (si rigano con una buona lima);
8) topazio;
9) corindone ⁽⁷¹⁾;
10) diamante ⁽⁷²⁾.

Attualmente alla scala di Mohs si preferiscono criteri di misurazione più attendibili che utilizzano per la valutazione della durezza di un materiale strumenti di "durezza, dimensioni e foggia speciali" come, ad esempio, i durometri ⁽⁷³⁾.

"Attenzione, però, a non confondere la durezza con la scarsa fragilità!" ⁽⁷⁴⁾.
Con il temine "durezza", infatti, ci si riferisce esclusivamente alla "resistenza che un materiale oppone alla penetrazione di una punta cioè alla scalfittura e non alla facilità che questi presenta a rompersi!" .
In questo caso si parla, infatti, di materiali fragili mentre "quei minerali che possono essere scalfiti da un unghia", come abbiamo appena scritto, vengono, invece, definiti teneri ⁽⁷⁶⁾.

"Un minerale può essere molto duro ma, allo stesso tempo, fragile: definiamo pertanto fragilità la facilità con cui un minerale, se colpito con forza, si sbriciola" ⁽⁷⁷⁾.

La tendenza che, invece, un minerale presenta "a rompersi secondo piani cristallografici ben definiti" è ascrivibile ad un'altra proprietà tipica di molti minerali cioè la sfaldatura.
È interessante vedere come alcuni minerali, anche molto duri, come ad esempio il diamante "si aprano con facilità quando vengono sottoposti ad una sollecitazione meccanica orientata" ⁽⁷⁸⁾.
Ma perché una pietra in alcuni casi si sfalda mentre, invece, in altri si "spacca"?
Che cosa crea la differenza?

Prima di tutto va puntualizzato che quelle che generalmente chiamiamo "pietre" non sono altro che frammenti di roccia costituiti da uno o più minerali ⁽⁷⁹⁾ e che ogni minerale è un solido cristallino che presenta "caratteristiche fisiche e una composizione chimica ben definite" ⁽⁸⁰⁾.
Rocce e minerali non vanno, pertanto, confuse.
Mentre, infatti, il termine roccia è un nome generico che si attribuisce a tutti quegli aggregati di elementi, anche molto diversi tra loro, che costituiscono la maggior parte della crosta terrestre, i minerali, invece, di cui abbiamo appena dato una definizione, sono semplicemente componenti essenziali delle rocce.
Una roccia, infatti, può essere costituita da uno o più minerali.
Il granito, ad esempio, è costituito da quarzo, feldspato e mica al contrario del marmo che rappresenta, invece, un esempio di "roccia fatta di un solo minerale: la calcite" ⁽⁸¹⁾.

Detto questo ritorniamo al nostro "frammento di roccia".
Come abbiamo già detto, molti minerali presentano una organizzazione reticolare tale per cui diventa possibile romperli soltanto se li si colpisce in un punto preciso della loro "struttura cristallina".
Anche il diamante, come abbiamo detto, per quanto sia stato classificato come uno dei minerali più duri in assoluto, "si apre con facilità quando viene sottoposto ad una sollecitazione meccanica orientata" ⁽⁸²⁾.
Perché?
Osservando al microscopio elettronico o a scansione (83) o per mezzo di una cristallografia ⁽⁸⁴⁾ la struttura di un cristallo notiamo che, al suo interno, gli atomi si distribuiscono secondo delle configurazione geometriche particolari.

"Esistono sette figure geometriche elementari, chiamate ‘sistemi cristallini', su cui possono basarsi questi motivi".

Tali figure sono quella cubica, quella tetragonale, quella trigonale, quella rombica o ortorombica, quella esagonale, quella monoclina e quella triclina ⁽⁸⁵⁾.

Ad esempio, gli atomi di alcuni cristalli, come i cristalli di sale, sono distribuiti in modo da formare "piccole unità cubiche distribuite ordinatamente le une accanto alle altre".

All'interno di ognuna di queste unità "le forze attrattive tra gli atomi sono molto grandi" mentre "quelle tra atomi di unità adiacenti sono deboli" ⁽⁸⁶⁾.
Nel momento in cui un minerale viene colpito saranno le forze più deboli a cedere per prime alle vibrazioni causate dal colpo ed è questo il motivo per cui un minerale si rompe secondo precise direzioni di sfaldatura quelle, cioè, in cui le lamine combaciano.
"Alcune specie presentano una sola direzione di sfaldatura altre invece possono averne anche due, tre, quattro o addirittura sei" ⁽⁸⁷⁾.

"La sfaldatura, però, non è una proprietà comune a tutti i minerali" ⁽⁸⁸⁾.

Molti minerali, infatti non si sfaldano ma si suddividono in frammenti irregolari. Parliamo in questo caso di frattura.
Cominciamo col dire che "la frattura in un minerale si presenta quando i legami fra gli strati di atomi sono pressoché uguali nelle varie direzioni" ⁽⁸⁹⁾.

A seconda dell'ordine che assumono i vari atomi all'interno del cristallo e dell'entità delle forze che li tengono uniti avremo piani di frattura differenti ⁽⁹⁰⁾.

In base a tali piani le fratture si distinguono in:
"scabra: segue superfici irregolari;
concoide: segue superfici lisce ma curve;
scagliosa: con superfici formate da particelle lamellari;
scheggiosa: con superfici cosparse di schegge o fibre;
terrosa: le superfici sono cosparse di minuscoli granuli" (91).

Il termine frattura lo troviamo spesso legato ad altre due proprietà molto importanti nei solidi quella di "fragilità" e quella di "resistenza".
La resistenza è quella proprietà che un corpo possiede "di sopportare un determinato stato di sforzo senza che avvengano rotture" ⁽⁹²⁾.
In altre parole, essa è la capacità che un corpo possiede di non lasciarsi rompere, spezzare, frammentare o deformare facilmente ⁽⁹³⁾.
L'aggettivo fragile si riferisce, invece, a un qualunque materiale che si rompa o si spezzi facilmente ⁽⁹⁴⁾ "senza andare incontro a deformazioni prima della rottura" ⁽⁹⁵⁾.
"Tanto che i loro frammenti talvolta possono essere ricomposti nella ricostruzione del corpo originale" ⁽⁹⁶⁾.

Quest'ultimo particolare è molto importante ai fini di una ulteriore distinzione.

Quando si parla di frattura, infatti, si può parlare di frattura duttile o di frattura fragile.

"La differenza si misura nell'entità delle deformazioni che le parti subiscono prima di essere staccate dal corpo originale" ⁽⁹⁷⁾.
Nella frattura fragile, come abbiamo detto, non si riscontra nessun tipo di deformazione plastica prima della rottura.
Per lo meno non in modo particolarmente evidente.
Le fratture fragili possono, talvolta, "verificarsi anche da sole" in assenza, cioè, di carichi applicati, semplicemente come conseguenza di "residui di tensione".
La frattura fragile è tipica di "molti elementi non metallici" che mancano di duttilità ma può accadere, comunque, che "in certe combinazioni di circostanza anche i metalli duttili subiscano fratture di tipo fragile" ⁽⁹⁸⁾.

Ma che cosa s'intende quando, invece, si parla di frattura duttile?
Cominciamo col dire che "I materiali duttili sono materiali molto più morbidi e che sono materiali che si deformano prima di rompersi" ⁽⁹⁹⁾.
La parola duttile deriva dal latino ducere "guidare", letteralmente "che si può condurre, tirare". Vengono, dunque, definiti duttili tutti quei corpi "che si possono piegare, allungare e ridurre in fili senza rompersi" ⁽¹⁰⁰⁾.

"Spesso i materiali duttili subiscono deformazioni ampie e permanenti prima di giungere alla rottura" ⁽¹⁰¹⁾.
Perché?
Anche in questo caso dobbiamo fare riferimento alla particolare disposizione che gli atomi assumono all'interno della materia.
Dall'analisi microscopica di una superficie metallica, si può notare, che al suo interno, è presente una struttura ‘a grani' caratterizzata da "zone di forma irregolare ben separate tra di loro che contengono un grande numero di atomi" ⁽¹⁰²⁾.
Cominciamo col dire che quando parliamo di grani ci riferiamo ai singoli cristalli in cui solidifica un materiale metallico.
Ciascuno di questi cristalli presenta una crescita indipendente "secondo un orientamento proprio fino a quando non viene a contatto col cristallo adiacente" ⁽¹⁰³⁾.
In tali zone di confine, dette ‘bordi dei grani', si riscontrano "distorsioni e difetti" nella struttura reticolare, dovuti, appunto, alla "diversa orientazione" che assume ogni cristallo rispetto a quelli vicini ⁽¹⁰⁴⁾.
Da qui la "forma irregolare" di cui si parlava prima.

Inoltre il grande numero di atomi, a cui prima facevamo riferimento, sono i cationi che, come abbiamo detto, si vengono a formare in conseguenza del particolare tipo di legame che si instaura tra i diversi elementi metallici.
Questi cationi occupano posizioni fisse e ordinate all'interno di ogni cristallo metallico o grano che essi vanno a costituire.
Gli "elettroni ceduti", invece, come abbiamo già detto, "vengono messi in comune" andando a costituire così una nuvola elettronica che si muove liberamente tra i cationi ⁽¹⁰⁵⁾.
I diversi strati di cristalli metallici, che vanno, poi, a formare il solido metallico, sono "capaci di slittare con relativa facilità l'uno sull'altro" ⁽¹⁰⁶⁾.
"La duttilità è dovuta dunque a tali fenomeni di scorrimento" ⁽¹⁰⁷⁾ e al fatto che "il mare di elettroni si adatta prontamente alla deformazione continuando a tenere gli atomi uniti" ⁽¹⁰⁸⁾.

La duttilità non va, però, confusa con la malleabilità.
L'aggettivo malleabile deriva dal latino malleus, martello e veniva usata in riferimento a tutti quei metalli che potevano essere lavorati con il martello ⁽¹⁰⁹⁾.
Attualmente tale aggettivo è usato ad indicare tutti quei solidi che hanno la "proprietà di lasciarsi ridurre in lamine più o meno sottili per compressione" a mezzo, ad esempio, di martello o laminatoio ⁽¹¹⁰⁾.
Entrambi i termini sottintendono, quindi, la proprietà del lasciarsi deformare prima di subire una rottura ma con una differenza.
Mentre la duttilità è quella proprietà che un corpo possiede di lasciarsi ridurre in fili, la malleabilità è, invece, quella proprietà che un corpo possiede di lasciarsi ridurre in lamine sottilissime ⁽¹¹¹⁾.

Duttilità e malleabilità rimandano ad un'altra proprietà molto importante nei solidi, l'elasticità.
"Se un oggetto o altro materiale solido, dopo essere stato deformato, invece di rompersi o di venire modificato permanentemente ritorna alla sua forma e alle sue dimensioni originarie, diciamo che è elastico".
Definiamo, pertanto, elasticità di un corpo la sua tendenza a ritornare nel suo stato originario dopo essere stato deformato da una forza.
Se la forza applicata ad un materiale supera il suo limite elastico, l'oggetto rimane, però, deformato permanentemente ⁽¹¹²⁾.
"Esistono alcuni materiali, come ad esempio l'argilla, che si deformano senza rompersi.
Tale proprietà viene definita plasticità" ⁽¹¹³⁾.

Ad ogni modo, ritornando all'esempio della "pietra" che si rompe, è importante sottolineare che ognuna delle parti in cui la pietra viene frantumata continua a conservare le proprietà caratteristiche della pietra.
Lo stesso dicasi per il metallo quando si deforma o nel caso dell'argilla quando viene modellata.
In tutti questi casi, cioè, la materia non va incontro a nessuna sostanziale modifica nella sua composizione chimica o nel suo stato fisico ma subisce soltanto alterazioni di tipo meccanico.

Mi spiego.

Se bruciamo un pezzo di legno possiamo osservare che esso si trasforma in cenere e in gas con la produzione di calore.
La cenere e il gas, tuttavia, non hanno più le proprietà del legno di partenza.
Questo significa che, all'interno della materia, si è avuta una trasformazione tale da alterare addirittura le proprietà stesse del legno.
Questo tipo di fenomeno che trasforma in modo così radicale la materia è chiamato, invece, reazione chimica ⁽¹¹⁴⁾.
Pertanto, definiamo reazione chimica quel processo in cui "una sostanza va incontro a trasformazioni sia nella composizione che nelle proprietà caratteristiche" (115).
Una reazione chimica può essere influenzata da diversi fattori "uno dei più importanti è senz'altro il calore" (116).

E per oggi mi fermerei qui!
Passiamo, dunque, alla parte pratica.

LEZIONE 5: PARTE PRATICA

Fino ad oggi abbiamo lavorato prevalentemente sulla metrica. Abbiamo gettato le basi, tuttavia, di quello che viene comunemente definito solfeggio ritmico: fino a questo momento abbiamo, inoltre, anteposto l'apprendimento uditivo a quello visivo! Privilegiando l'orecchio all'occhio!
Per studiare il solfeggio è, invece, importante allenare anche la nostra memoria visiva.
Dobbiamo essere in grado, cioè, di collegare uno stimolo visivo ad un suono. Di passare da una figura ritmica ad un'altra riproducendone le sonorità all'impronta!
La prima cosa che dobbiamo fare, dunque, è imparare come si trascrivono graficamente determinate sensazioni acustiche.

Oltre all'intensità, un altro parametro molto importante in musica è la durata.
La durata di un suono, come dice stesso la parola, è quel parametro che si riferisce "all'estensione e alla continuità di un suono nel tempo" ⁽¹¹⁷⁾.

Un suono, cioè, può essere

• forte o debole ed allora parliamo di intensità;
• oppure lungo o corto ed allora parliamo di durata;

Quando vogliono indicare per quanto tempo deve durare un suono, i compositori fanno uso di particolari simboli grafici chiamati: valori musicali o note.

Vi ricordate gli esempi sul metro musicale che abbiamo fatto nella lezione 3? Oggi inseriamo un elemento nuovo.
Negli esercizi fatti nella lezione tre avevamo indicato le pulsazioni con delle freccette, in quelli che faremo oggi, per indicare le pulsazioni, al posto delle freccette, useremo delle figure ritmiche, o meglio ne useremo una in particolare: la semiminima.
La semiminima, dunque, in questo caso, è stata scelta come unità di movimento, cioè come quella figura di valore che da sola riempie lo spazio di un intero movimento.

Riscriviamo, dunque, i nostri esempi mettendo questa volta al posto di ogni freccetta una semiminima.
Ne consegue che anche al denominatore della frazione che metteremo all'inizio di ogni frase, al posto della freccetta, scriveremo una semiminima. Per cui avremo:

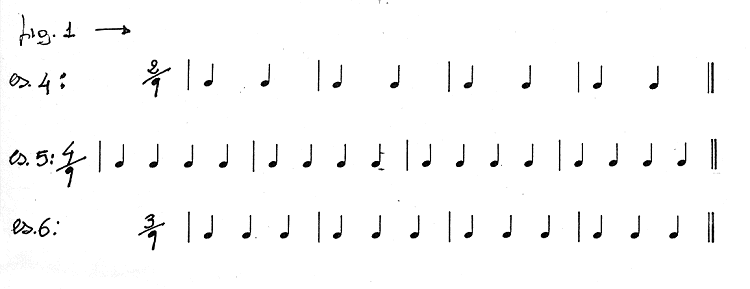
Da quanto detto deduciamo dunque che, come unità di movimento, possiamo scegliere anche altre note, oltre alla semiminima, e così è infatti.
Per capire meglio questo argomento dobbiamo prima, però, studiare le altre figure di valore nonché le relazioni spazio/temporali che esistono tra di loro.

Ritorniamo, invece, adesso ai nostri esempi e solfeggiamoli.


Come avete potuto notare, da un punto di vista acustico, non è cambiato assolutamente niente rispetto agli esempi riportati nella lezione tre.
Se, infatti, leggiamo un brano, "davanti a un uditorio", sia che questo brano sia scritto in corsivo o che sia scritto in stampatello, il messaggio che arriverà all'orecchio di chi ascolta sarà sempre lo stesso ⁽¹¹⁸⁾.
Mi spiego, se vogliamo che il suono duri per una intera pulsazione, sia che decidiamo di usare una freccia o che decidiamo di usare un qualunque altro simbolo grafico per indicare l'unità di movimento, l'effetto acustico sarà sempre lo stesso.

Tuttavia, ci tengo a puntualizzare che tale esercizio anche se acusticamente coincide con quello fatto nella lezione tre non è esattamente la stessa cosa. In questo caso, infatti, noi non stiamo "cantando" la metrica ma la ritmica: se compriamo un nastro della lunghezza di un metro, il nastro coinciderà con il metro ma nastro e metro non sono la stessa cosa. Abbiamo usato il metro come punto di riferimento per dare al nastro la lunghezza (nel nostro caso la durata) desiderata!
Non ritengo utile, per il momento, soffermarmi ulteriormente su questo argomento. Passerei, pertanto, allo studio delle altre figure di valore!

Se decidiamo che un suono ci deve durare per due movimenti anziché per un solo movimento allora dovremo scegliere per rappresentare questa nostra "esigenza ritmica", un simbolo diverso dalla semiminima che, essendo stata scelta come unità di movimento, ci indica che il suono deve durare soltanto per il tempo di un unico movimento.
In base a quale criterio sceglieremo il nostro nuovo simbolo ritmico?
"I simboli di note e pause non hanno una durata prefissata e assoluta, ma solo un rapporto preciso di durata relativa: vale a dire che ciascun simbolo rappresenta il doppio del valore e viceversa la metà del valore di altri due simboli".
È come se essi fossero "tutti inseriti in una sorta di ‘albero genealogico' in progressione binaria discendente.
Sappiamo che ogni simbolo si trova fra altri due, di cui rappresenta rispettivamente la metà e il doppio" ⁽¹¹⁹⁾.

Diamo, quindi, uno sguardo al nostro "albero genealogico" e vediamo qual'è il simbolo grafico che vale il doppio della semiminima.
La nota che dobbiamo, dunque, usare, nel nostro caso, per indicare che il suono deve durare per due movimenti anziché per uno è la minima, in quanto nella gerarchia dei valori ritmici essa ha un valore di durata che corrisponde al doppio di quello della semiminima.
Se, invece, vogliamo che il suono ci duri per quattro movimenti allora sceglieremo, come simbolo grafico, la semibreve la quale, sempre in base alla gerarchia dei valori ritmici, rappresenta un valore di durata pari a 2 minime e quindi a 4 semiminime.

E se, invece, vogliamo che il suono ci duri per tre movimenti?
In questo caso ricorreremo ad un piccolo "accorgimento": il punto di valore.
Otterremo così la minima con il punto.
Definiamo "punto di valore un punto che collocato dopo la testa della nota ne incrementa la durata di metà del suo valore" ⁽¹²⁰⁾.

Possiamo adesso capire meglio quanto dicevo ad inizio lezione a proposito del fatto che, indipendentemente dal simbolo grafico scelto come unità di movimento, l'effetto sonoro rimane invariato.
Se, infatti, come unità di movimento, scegliamo una minima anziché una semiminima ne avremo come conseguenza che dovremo far durare il suono per un intero movimento ogni qual volta incontriamo una minima anziché quando incontriamo una semiminima come abbiamo fatto fino adesso. Se vogliamo che il suono ci duri per due movimenti prenderemo dal nostro "albero genealogico musicale" quella figura che si trova immediatamente al di sopra della minima con valore di durata doppio di quello della minima, vale a dire, la semibreve.

È chiaro che, se decidiamo di usare la minima come unità di movimento, questo dovrà essere segnalato.
Per cui al denominatore della frazione posta all'inizio dei nostri esempi ritmici scriveremo il simbolo di una minima anziché quello della semiminima.

Gli esempi verranno scritti nel seguente modo:

Come potete notare, solfeggiandoli, ciò che cambia rispetto agli esempi precedenti è soltanto il modo in cui l'esempio viene trascritto graficamente mentre l'effetto acustico rimane identico.
Ricordate quanto vi ho detto a proposito del corsivo e dello stampatello?

Ma allora, se è vero che una nota può avere valore di durata diverso a seconda della sua relazione con l'unità di movimento, perché diciamo che la semiminima vale 1/4, la minima vale 2/4 etc. ?

Che cosa significano queste frazioni?

Disegniamo un cerchio a cui decidiamo di dare il nome di semibreve e il valore di un intero.

Dividiamo questo cerchio in due parti uguali e ad ognuna di queste due parti decidiamo di dare il nome di minima ed il valore di 1/2;
due minime equivalgono, dunque, al valore di un intero.
Adesso, invece, dividiamo l'intero in quattro parti e ad ognuna di queste 4 parti diamo il nome di semiminima ed il valore di 1/4, in quanto rappresenta la quarta parte di un intero; ci vogliono, dunque, due semiminime per equiparare il valore di una minima e quattro semiminime per equiparare il valore di un intero!
Questo è il motivo per cui solitamente ad una minima si dà il valore di 2/4 e ad una semibreve il valore di 4/4.

Quindi la semiminima vale 1/4 perché rappresenta la quarta parte di un intero.

A questo punto riprendiamo i nostri esercizi e riscriviamo in modo ancora più preciso le nostre frazioni:

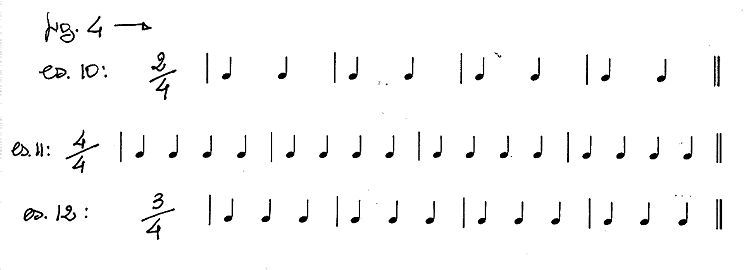
Tale frazione, comunemente definita indicazione di tempo ci dice che:

• l'accento metrico cade ogni 2, 4 o 3 pulsazioni (ogni battuta è costituita, cioè, rispettivamente da due, quattro o tre movimenti)
• e che la figura ritmica scelta come unità di movimento è il quarto cioè la semiminima;

quindi, ricapitolando,

• mentre il numeratore della frazione che troviamo all'inizio di un brano musicale indica quante pulsazioni sono presenti all'interno di ogni battuta (ne indica, cioè, gli accenti principali) ⁽¹²¹⁾;
• il denominatore indica quale figura di valore è stata scelta come unità di movimento.

Abbiamo detto che per unità di movimento s'intende quella figura che da sola riempie lo spazio di un intero movimento.

Che cosa s'intende, invece, per unità di battuta?

Semplice. Per unità di battuta si intende quella figura che da sola riempie lo spazio di un'intera battuta.

Quindi mentre sia nel 2/4, che nel 4/4, che nel 3/4 l'unità di movimento sarà sempre la semiminima, come unità di battuta avremo, invece, rispettivamente:

• la minima nel caso di una esercizio in 2/4 (cioè 2 movimenti da 1/4; 1/4 + 1/4 = 2/4);
• la semibreve nel caso di un esercizio in 4/4 (cioè 4 movimenti da 1/4; 1/4 + 1/4 + 1/4 + 1/4 = 4/4);
• la minima con il punto nel caso di un esercizio in 3/4 (cioè 3 movimenti da 1/4; 1/4 + 1/4 + 1/4 = 3/4);

Anche il silenzio in musica ha una durata ben precisa che, allo stesso modo dei suoni, viene indicata con apposite figure di valore chiamate figure di pausa.

Nella figura che segue sono raffigurate le figure di pausa relative alle note che abbiamo studiato fino a questo momento:

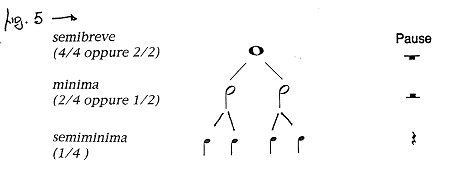
E per oggi mi fermo qui! ⁽¹²²⁾.

La prossima volta riprenderemo quanto detto in questa lezione sviluppandolo e articolandolo con esempi di natura gradualmente più complessa.

NOTE:
(1) Paul G. Hewitt, Fisica per concetti, Bologna: Zanichelli, 2001 (1987), p. 248.
(2) Arrigo Amadori, "Corso di cultura scientifica di base", www.arrigoamadori.com/lezioni/CorsiEConferenze/Astrofili1/ast-002-24-10-03-pre.htm
(3) Paul G. Hewitt, op.cit., p. 248.
(4) Arrigo Amadori, op. cit.
(5) Paul G. Hewitt, op.cit., p. 248.
(6) Robin Kerrod e Dr. Sharon Ann Holgate, L'enciclopedia attiva della scienza, Trieste: Editoriale Scienza, 2003 (2002), p. 10.
(7) Gerhard Staguhn, Breve storia dell'atomo, Milano: Adriano Salani Editore, 2002 (2000), pp. 84-85.
(8) B. Alberts, D. Bray, A. Johnson, J. Lewis, M. Raff, K. Roberts, P. Walter, Biologia molecolare della cellula, Bologna: Zanichelli, 2004 (1983), p. 53.
(9) Ibid. p. 53.
(10) Vanna Comaschi, "Il legame chimico", http://www.itg-rondani.it/dida/chimica/modulo3/ud3_1/ud3_1pag1.htm
(11) David L. Nelson, Michael M. Cox, I principi di biochimica di Lehninger, Bologna: Zanichelli Editore, 2002 (1982), p. 61.
(12) Ibid. p. 61.
(13) B. Alberts, D. Bray, A. Johnson, J. Lewis, M. Raff, K. Roberts, P. Walter, op.cit., p. 53.
(14) Vanna Vannucchi, "Passaggi di stato", http://www.bdp.it/~trends10/targeon/vanna/passaggi.htm
(15) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 16.
(16) "Geologia: chiedi all'esperto", http://www.vialattea.net/esperti/geo/vetro.htm
(17) Esistono in natura diverse sequenze reticolari. A tale proposito
vedi i 14 reticoli di Bravais ("Solidi", solidi1.pdf, p. 4).
(18) "Solidi", solidi1.pdf, pp. 3-5.
(19) "I minerali: la struttura cristallina", http://www.ips.it/scuola/concorso/minerali/minerali.htm
(20) A proposito di perfezione… segue l'elenco di alcuni dei più frequenti tra i difetti reticolari che è possibile riscontrare all'interno delle diverse strutture cristalline: vacanza, impurità sostitutiva; atomo interstiziale, impurità interstiziale, dislocazione ("Solidi", solidi1.pdf, p. 5).
(21) Vanna Vannucchi, op.cit.
(22) "I liquidi e i solidi", http://venus.unive.it/chem00/capitoli/19.htm
(23) "Geologia: chiedi all'esperto", op.cit.
(24) Amorfo è un termine che deriva dal greco ed è un composto di a- e morphe. Dove: a-, detto alfa o "a" privativo", svolge la funzione che, nel greco classico, aveva il cosiddetto "alfa negativo ". Indica, quindi, mancanza, assenza. Mentre morphe significa "forma". Amorfo vuol dire, dunque, "privo di forma" (Nicola Zingarelli, Il nuovo Zingarelli: vocabolario della lingua italiana, Bologna: Nicola Zanichelli, 1983, XI edizione).
(25) "Geologia: chiedi all'esperto", op.cit.
(26) Philip Ball, H2O: una biografia dell'acqua, Milano: Biblioteca Universale Rizzoli 2000 (1999), p. 175.
(27) Vanna Vannucchi, op.cit.
(28) "Il vetro è un liquido o un solido", http://www.universitor.it/leggiarticolo.php?a=1&sez=50&art=420
(29) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 10.
(30) "I liquidi e i solidi", op.cit.
(31) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 10.
(32) "Introduzione", http://dcssi.istm.cnr.it/CORSO%20IPERTESTUALE/StatoSolido/Modelli_4/cap4_introduzione.htm
(33) Vanna Comaschi, "Il legame metallico", http://www.itg-rondani.it/dida/chimica/modulo3/ud3_1/ud3_1pag1.htm
(34) Gerhard Staguhn, op.cit., p. 79.
(35) "Lo stato solido", http://www.scibio.unifi.it/triennali/firenze_3/stato_solido.htm
(36) Vanna Comaschi, "Il legame metallico", op.cit.
(37) Gerhard Staguhn, op.cit., p. 80.
(38) Vanna Comaschi, "Il legame metallico", op.cit.
(39) "Legami chimici", legami chimici2.pdf p. 27.
(40) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 46.
(41) Vanna Vannucchi, op.cit.
(42) "Solidi", solidi1.pdf, p. 1.
(43) Vanna Vannucchi, op.cit.
(44) "Solidi", solidi1.pdf, p. 1.
(45) Vanna Vannucchi, op.cit.
(46) "Solidi", solidi1.pdf, p. 2.
(47) Vanna Vannucchi, op.cit.
(48) "Solidi", solidi1.pdf, p. 2.
(49) Philip Ball, op.cit., p. 175.
(50) Arrigo Amadori, op. cit.
(51) Gerhard Staguhn, op.cit., pp. 85-86.
(52) La parola "friabile" deriva dal latino friare, "sminuzzare". Essa si riferisce a "tutto ciò che, per scarsa coesione, può ridursi in briciole, farina, polvere e simili" (Nicola Zingarelli, op.cit.).
(53) "Elenco ragionato delle raccomandazioni NORMAL", http://www.tine.it/normal/normal.htm
(54) "Acciaio", http://it.wikipedia.org/wiki/Acciaio
(55) "Alla scoperta del cemento", http://www.italcementi.it/newsite/cemento.htm
(56) "Il restauro del mobile antico", http://web.tiscali.it/restauroantico/restauro_ceramica.htm
(57) "Materie plastiche", http://it.wikipedia.org/wiki/Materie_plastiche
(58) "Storia dei tessuti", http://www.edel2000.it/club/TESstoria.htm
(59) Per proprietà di un materiale s'intende "l'insieme delle caratteristiche comuni a un gruppo di materiali o tipiche di un determinato materiale. Agli effetti pratici si possono distinguere proprietà di natura fisico-chimica, meccanica e tecnologica" ("Le proprietà dei materiali da costruzione", http://www.racine.ra.it/ungaretti/SeT/macvapor/propmate.htm)
(60) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 14.
(61) Alberto Bargellini, Maria Fratello, Luciana Monfroni, Osservazioni ed elementi di scienze naturali, Milano: Casa Editrice Carlo Signorelli, 1972, vol. III, p. 134.
(62) "I minerali: proprietà chimiche e fisiche", http://www.ips.it/scuola/concorso/minerali/propriet.htm
(63) "Le proprietà delle gemme", http://www.minerali.it/gemme/gemmeproprieta.htm
(64) "Gemme", http://www.nigilab.com/cgem.htm
(65) "Le proprietà delle gemme", op.cit.
(66) "Gemme", op.cit.
(67) "Le proprietà delle gemme", op.cit.
(68) "I minerali: proprietà chimiche e fisiche", op.cit.
(69) "Armonie di forme e colori: i minerali", http://www.thais.it/mineralogia/Introduzione.htm
(70) "I minerali: proprietà chimiche e fisiche", op.cit.; "Le proprietà delle gemme", op.cit.
(71) Il corindone nella sua "varietà rossa è il rubino, in tonalità blu è lo zaffiro" "Gemme", op.cit.
(72) "Nozioni fondamentali", http://www.ars2000.it/geologia.htm
(73) "Proprietà dei materiali e normativa", http://users.unimi.it/~spoli/petapp/proptec.doc.
(74) "Gemme", op.cit.
(75) "Proprietà meccaniche", http://www.racine.ra.it/ungaretti/SeT/macvapor/propmec.htm
(76) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. III, p. 133.
(77) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 13.
(78) "Le proprietà delle gemme", op.cit.
(79) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. III, p. 130.
(80) "I minerali: la struttura cristallina", op.cit.
(81) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. III, pp. 146-147.
(82) "Le proprietà delle gemme", op.cit.
(83) Francesco Iacoviello, "Comportamento a temperatura elevata", materiali_metallici_4.pdf p.32.
(84) "I minerali: la struttura cristallina", op.cit.
(85) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 16.
(86) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. II, pp. 62-63.
(87) "Sfaldatura", http://it.wikipedia.org/wiki/Sfaldatura
(88) "Armonie di forme e colori: i minerali", op.cit.
(89) "Frattura (mineralogia)", http://it.wikipedia.org/wiki/Frattura_%28mineralogia%29
(90) "Le proprietà delle gemme", op.cit.
(91) "Frattura (mineralogia)", op.cit.
(92) "Resistenza", http://www.sapere.it/gr/ArticleViewServlet?tid=1141106&rid=1141106&from=ArticleViewServlet
(93) Nicola Zingarelli, op.cit.
(94) Ibid.
(95) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 13.
(96) "Fragilità a basse temperature", http://ulisse.sissa.it/SingleQuestionAnswerProfile.jsp?questionCod=92799014
(97) Ibid.
(98) "Frattura fragile", http://www.failure-analysis.it/IT02140000.asp?D=5
(99) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 13.
(100) Nicola Zingarelli, op.cit.
(101) "Fragilità a basse temperature", op.cit.
(102) "Il legame chimico", chimica6.pdf, p. 18.
(103) "Proprietà meccaniche - Influenza della temperatura", http://www.ge.infn.it/~vaccaron/dispense_files/alessandria/CORSO%20MATERIALI%20CON%20LINK1.doc
(104) "Proprietà meccaniche - Influenza della temperatura", op.cit.
(105) Vanna Comaschi, "Il legame metallico", op.cit.
(106) "Lo stato solido", op.cit.
(107) "Il legame chimico", chimica6.pdf, pp. 18-19.
(108) "Legame nei solidi e proprietà elettroniche", http://www.chimdocet.it/inorganica/file26a.htm
(109) Nicola Zingarelli, op.cit.
(110) "Metalli", http://artisans.ombra.net/tecniche/metalli.htm
(111) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. III, p. 134; "Legami chimici", legami chimici2.pdf p. 34.
(112) Robin Kerrod e Dr. Sharon Ann Holgate, op.cit., p. 13.
(113) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. III, p. 134.
(114) Ibid. vol. II, pp. 64-65.
(115) William K. Purves, David Sadova, Gordon H. Orians, H. Craig Heller, Biologia: la cellula, Bologna: Zanichelli, 2001 (1998), p. 22.
(116) Alberto Bargellini, Maria Fratello, Luciana Monfroni, op.cit., vol. II, p. 76.
(117) Patrizia Carriere, Aurora Lerardi, Insegar musica giocando: Guida didattica per l'educazione al suono e alla musica nella scuola elementare, Milano: Ricordi, 1992, p. 26.
(118) Nicoletta Caselli, Manuale di teoria musicale: con riferimento alla musica moderna, Milano: Nuova Carish, 1993, p. 28.
(119) Ibid., pp. 14-18.
(120) Ibid., p. 15.
(121) Ibid., p. 26.
(122) Rimando a qualsiasi testo di musica per uno studio più approfondito della scrittura delle note e delle relative pause. Per quanto riguarda gli esempi ritmici un qualunque testo di solfeggio va bene. Vi consiglio, tuttavia, di scegliere un testo che abbia un supporto sonoro. Rimando, inoltre, alle lezioni di batteria di Alex Barberis (http://www.jazzitalia.net/Artisti/alexbarberis.asp) che potete trovare su www.jazzitalia.net alla pagina http://www.jazzitalia.net/lezioni.asp

© 2004, 2005 Jazzitalia.net - Sandra Evangelisti - Tutti i diritti riservati

© 2000 - 2024 Tutto il materiale pubblicato su Jazzitalia è di esclusiva proprietà dell'autore ed è coperto da Copyright internazionale, pertanto non è consentito alcun utilizzo che non sia preventivamente concordato con chi ne detiene i diritti.

Questa pagina è stata visitata 10.449 volte Data pubblicazione: 27/11/2005 Home |  Articoli |  Comunicati |  Io C'ero |  Recensioni |  Eventi |  Lezioni |  Gallery |  Annunci Artisti |  Saranno Famosi |  Newsletter |  Forum |  Cerca |  Links | Sondaggio |  Cont@tti